|
 НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ
Григоренко А.М. Г83 © Некоторые вопросы теории технической информации.
- М.: Издательство «ЮБЕКС», 1998-112 JSBN №5-7158-0158-6
В монографии изложены вопросы теории и практики в
создании различных информационно- измерительных и управляющих систем. Материал, изложенный в книге,
позволит специалистам, создающим и использующим информационно- измерительные системы и системы
автоматического контроля и управления, обеспечить максимальную эффективность использования таких
систем, достоверность получаемой информации, расширить области их применения. Ряд вопросов,
рассмотренных в книге, имеет фундаментальный характер и рекомендуется преподавателям и студентам,
специализирующимся в области теории связи, технической информации, технической кибернетики и пр. |

ВВЕДЕНИЕ
Нет необходимости доказывать, что измерительная
информация является одной из основных составляющих в процессе создания и использования современной
техники, а также во множестве других областей человеческой деятельности. Действительно, любая более-менее
сложная техника, имеет системы автоматического управления и контроля, а такие отрасли человеческой
деятельности, как метеорология, метрология и пр. вообще только тем и заняты, что собирают и обрабатывают
измерительную информацию. Наверное, без особого преувеличения, можно сказать, что измерительная
информация является одной из основ современной цивилизации.
Однако вряд ли можно сказать, что
теоретические основания в области измерительной информации находятся в полном порядке и устраивают
практиков. Предлагаемые благосклонному читателю результаты исследований могут оказаться вполне
полезными, особенно при расчете потоков измерительной информации с учетом ее метрологической точности
и достоверности как при создании и использовании измерительно-информационных систем (ИИС), так и систем
автоматического контроля и управления с использованием ИИС. Ряд положений разработанных автором и
изложенных в данной книжке апробированы на практике при испытаниях авиационной техники и получили
положительную оценку у авторитетных специалистов.
В книгу включены вопросы определения частот
опроса изменяющихся во времени и пространстве параметров, системного анализа погрешностей ИИС с
учетом погрешности дискретизации, борьбы с аномальными измерениями и некоторые другие вопросы. Кроме
того, учитывая, что часто ИИС являются элементом систем автоматического управления, возникла задача
уточнения и некоторых вопросов теории обратной связи как основы таких систем. Поскольку сама по себе
теория измерительной информации, как и теория обратной связи, существуют давно, то возникла
необходимость определенной критики имеющегося теоретического базиса. Кратко описаны некоторые
примеры практической реализации предлагаемых теоретических положений.
Автор надеется, что результаты этой работы
окажутся не бесполезными, и будет благодарен за конструктивную критику.
ГЛАВА 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
ИИС
Иформационно-измерительная система
является сложным объектом техники имеющая ряд характеристик, основными из которых являются
информационные и метрологические. Основные информационные характеристики следующие:
- информационный поток от объекта на систему в целом и на ее отдельные
элементы;
- производительность элементов ИИС;
- требуемые объемы запоминающих
устройств элементов ИИС.
Основными метрологическими
характеристиками ИИС являются точность и достоверность измерений. Информационный поток от объекта
зависит от его динамических характеристик и требований к точности измерений. В этом плане он не зависит
от ИИС и является заданной величиной. Однако, как правило, этот поток является в значительной степени
избыточным. Снижение избыточности может быть достигнуто:
- адаптацией структуры ИИС к решению конкретных задач и,
соответственно, изменением перечня подключаемых датчиков и других источников информации, их числа и
частот их опроса;
- обоснованием действительно необходимых норм точности;
-
обоснованием действительно необходимого числа замеров в единицу времени (частоты опроса).
Что касается обоснования перечня и числа
опрашиваемых датчиков, а также требуемых норм точности, то они определяются разработчиками ИИС, исходя
из конкретных задач применительно к конкретному объекту, и обсуждение их в рамках настоящей работы не
представляется необходимым.
Здесь мы рассмотрим вопросы определения
частот опроса. Вопрос этот не новый. Началом формирования теоретической базы определения частот опроса
(или теории дискретизации) обычно считают работы Котельникова В.А.[1] и Шеннона [2]. Имеются и ряд других
работ по этому вопросу. Однако их теоретический анализ и анализ их практического применения показывает,
что эффекта от существующей теоретической базы практически нет никакого. Более подробно критика ее
изложена в ПРИЛОЖЕНИИ 1. В связи с этим, до настоящего времени частота опросов определялась весьма
приближенно и, как правило, интуитивно, на основании опыта специалистов и, в лучшем случае ,
экспериментально. При этом частота опросов становится существенно избыточной и может привести к таким
требованиям к аппаратуре, что создание ИИС становится проблематичным или, по крайней мере, она
становится существенно более громоздкой и дорогой. Занижение же частот опроса приводит к
метрологической недостоверности результатов измерений. Далее будет рассмотрены вопросы определения
частоты дискретизации.
ГЛАВА 2. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ
ДИСКРЕТИЗАЦИИ
1. Методы дискретизации и восстановления
сигналов после дискретизации можно разделить на несколько групп в зависимости от принятых признаков
классификации. Выбираются следующие признаки классификации[3]:
- регулярность отсчетов;
- критерий оценки точности
дискретизации и восстановления;
- базисные функции;
- принцип приближения.
В соответствии с признаками регулярности
отсчетов можно выделить две основных группы методов: равномерную и неравномерную. Методы равномерной
дискретизации нашли наиболее широкое применение. Это объясняется тем, что алгоритмы дискретизации и
восстановления достаточно просты. Однако, из-за несоответствия априорных характеристик измеряемого
параметра характеристикам модели обработки, возможна значительная избыточность отсчетов. Из методов
неравномерной дискретизации известны две группы - адаптивные и программируемые.
Адаптивные методы позволяют уменьшить
избыточность информации, однако реализация их связана с рядом трудностей, а именно:
-
сложность алгоритмов;
- необходимость предсказания;
- в целом канал должен быть
рассчитан на максимальный поток информации, что снижает преимущества этого метода.
Вследствие этих и других недостатков метод
адаптивной дискретизации не нашел широкого применения и в дальнейшем рассматриваться не будет.
При программных методах дискретизации
изменение частоты опроса производится в соответствии с заранее составленной программой измерений. В
пределах данного этапа измерений он сводится к равномерной дискретизации.
2. Из критериев оценки точности известны
максимальный, среднеквадратичный, интегральный и вероятностно-зональный [ 3 ].
Наиболее широко используется
вероятностно-зональный критерий, определяемый соотношением:
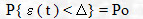 ( 2. 1 ),
( 2. 1 ),
где
Ро - допустимая вероятность того, что погрешность не превысит значения
 . Обычно считают Ро заданной и в соответствии с [ 4 ] ее можно принять 0.05. В этих условиях
задаются величины только
. Обычно считают Ро заданной и в соответствии с [ 4 ] ее можно принять 0.05. В этих условиях
задаются величины только
 , которые в практических случаях
выражаются , как правило, приведенными к максимальной величине диапазона измерения в процентах.
, которые в практических случаях
выражаются , как правило, приведенными к максимальной величине диапазона измерения в процентах.
3. Задача дискретизации неразрывно
связана с задачей восстановления функции. При этом решетчатой функции, представленной выборками,
необходимо поставить в соответствие непрерывную функцию которая отличалась бы от исходной функции на
величину не превышающую заданную погрешность то есть: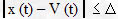 ( 2.2. )
( 2.2. )
Функция V(t) - воспроизводящая
функция. В качестве воспроизводящих функций могут применяться ортогональные ряды (Ряды Фурье,
Котельникова и т.д.), степенные полиномы и т.п. При обработке на ЭВМ наибольшее распространение получили
степенные ряды, благодаря достаточно простым алгоритмам их реализации. Восстанавливающие функции
названы базисными, поскольку от выбора этих функций в значительной мере зависит метод обоснования
характеристик дискретизации и восстановления информации.
4. По принципу приближения выделены три
группы методов:
- интерполяционные;
- экстраполяционные;
-
комбинированные.
Преимущество интерполяционных методов
является их более высокая точность, но они вносят задержку на период дискретизации, поэтому появляется
дополнительная динамическая погрешностью Экстраполяционные методы применяются в том случае, если ИИС
входит в замкнутый контур управления объектом, когда временные задержки недопустимы. Но они требуют
большую частоту отсчетов и, следовательно, большего потока информации. В условиях конкретных задач
могут применяться комбинированные методы.
Таким образом, далее под дискретизацией
будет пониматься, прежде всего, программно-адаптивная (равномерная) дискретизация. Критерием точности
принимается вероятностно-зональный критерий. Будет определен выбор базисной функции и рассмотрены
вопросы как интерполяции, так и экстраполяции.
5. Измеряемые параметры зависящие от времени
можно отнести к аналитическим функциям. Они ограничены по величине, имеют, как правило, экстремумы, не
имеют разрывов ни первого, ни второго рода ни у самой функции, ни у ее производных. Необходимо отметить,
что некоторые параметры могут иметь настолько быстрые изменения, что могут приниматься за разрывы
первого рода. Однако это является исключением из общего правила и может в отдельных случаях
соответствующим образом учитываться.
6. Поскольку речь идет о частоте
дискретизации, то, очевидно, что в первую очередь должен быть поставлен вопрос о динамичности функции.
Динамичность функции может быть выражена
при помощи следующих характеристик:
- автокорреляционных функций;
- частотного спектра;
- величин максимальных
производных функции.
Чаще всего ИИС проектируется для объектов с
параметрами, динамические характеристики которых точно неизвестны. Например, ИИС для испытаний
мобильной техники (в частности летательных аппаратов) могут применяться для различных типов техники и
различных этапов испытаний. В связи с этим определить стохастические или спектральные характеристики
измеряемых параметров не представляется возможным, поскольку они могут быть определены в процессе
испытаний, то есть тогда, когда ИИС уже изготовлена. Кроме того, реальные измеряемые параметры можно
отнести к не стационарным процессам, априорная неопределенность которых делает невозможным получение
представительной выборки. В связи с чем, применение стохастических методов вообще и
автокорреляционного анализа в частности не представляется возможным. Поскольку автокорреляционная
функция сопряжена со спектральной плотностью по формуле Винера-Хинчина, то же можно сказать и о
спектральном анализе. Исходя из этого, предпочтительным является использование в качестве
характеристик динамичности величин максимальных производных. Анализ практики реальных измерений
показывает, что измеряемые параметры имеют как минимум до второй производной максимальные величины
которых несложно получить расчетным, экспериментальным или иным путем. И даже интуитивные
предположения об их величине сделанные специалистом в данной области достаточно достоверны.
Такой подход имеет то преимущество, что
динамика процесса выражается через достаточно наглядные характеристики. Эти характеристики имеют
определенное техническое содержание. Например, при измерении высоты первая производная это не что иное,
как скороподъемность, а вторая производная - вертикальная перегрузка. Таким образом, зная максимально
допустимую вертикальную перегрузку можно определить частоту опроса датчика высоты.
7. Поскольку применение стохастических
методов не представляется возможным, то должен быть применен математический аппарат, построенный на
применении детерминированных функций. Однако измеряемые параметры являются априорно неопределенными,
а, следовательно, случайными. Выход здесь один, привести априорно не известную, случайную функцию к
априорно известной функции отвечающей тому требованию, чтобы их динамические характеристики были
одинаковы. Очевидно, что при этом и частота опроса у них будет одинакова.
Требования к такой функции следующие:
- во-первых, она должна максимально соответствовать характерным
особенностям реальных параметров;
- во-вторых, иметь достаточно простое
выражение.
Как известно, любая аналитическая функция
может быть разложена в ряд Фурье. Поэтому синусоида является достаточно удобной функцией для
сопоставления с аналитической функцией отображающей измеряемый параметр. В практическом плане
немаловажно и то, что некоторые параметры достаточно близки к синусоиде. Например, колебания элементов
конструкции летательного аппарата.
|
|
|
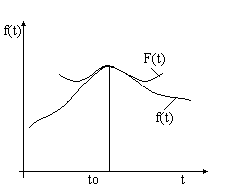
Рис.1 |
Идея метода заключается в следующем [Рис.1]. В момент
времени t0, соответствующий локальному экстремуму функции f(t), в котором |f"(t)| максимальна, функция f(t) аппроксимируется синусоидой F(t). При этом,
|F"(t)|max=|f"(t)|max. Поскольку момент времени t0,
вообще говоря, не определен, то предполагается, что, в условиях измерения данного параметра, возможно
такое событие, при котором в некоторый момент времени t0 вторая производная достигнет своего
максимума. Причём из условий измерения параметра она не может выть больше этого
максимума, т.е.:
{| f "(t)|} 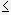 |f"(t)max|.
|f"(t)max|.
Момент времени t0 удобно принять в
качестве t = 0 , при этом F(t) = max . То есть, F(t) есть ни что иное как косинусоида. При
стремлении окрестности t0 к нулю, | F(t) - f(t) |
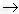 0 . Следовательно, в
окрестности t0 F(t) является аппроксимирующей функцией. В связи с этим, метод назван методом
аппроксимирующей косинусоиды.
0 . Следовательно, в
окрестности t0 F(t) является аппроксимирующей функцией. В связи с этим, метод назван методом
аппроксимирующей косинусоиды.
Амплитуда косинусоиды, при заданной | F"(t) |max,
однозначно связана с частотой и может быть любой величины, в том числе и равной диапазону погрешности
измерения данного параметра. В свою очередь, имея частоту косинусоиды можно
определить частоту ее опросов, из условия 100% погрешности возможного искажения этой косинусоиды в связи
со стробоскопическим эффектом, который будет рассмотрен ниже. В дальнейшем
можно будет привести полученные формулы к виду удобному для практического использования.
8. Итак F(t) =cos( t +
t +
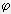 ). Так как t0 принимается за начало отсчета и при этом F(t) максимально, то
). Так как t0 принимается за начало отсчета и при этом F(t) максимально, то
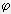 =0. Тогда F(t) = cos
=0. Тогда F(t) = cos t.
t.
Учитывая что | f" (t) max | = | F" (t)max | и F"(t)= 2 cos
2 cos t то |f"(t)max | =
t то |f"(t)max | =
 2 cos
2 cos t.
t.
В точке t =0 | F"(t) | максимален, при этом |F"(t)max| =
 2 .
2 .
Отсюда:
 2 = |f"(t)max|
, следовательно:
2 = |f"(t)max|
, следовательно:
 =
= | f"(t)max | .
| f"(t)max | .
Тогда
формула аппроксимирующей синусоиды примет вид: F(t)=cos(( |f"(t)max|)
|f"(t)max|)
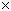 t)
.
t)
.
Как указывалось выше, амплитуда косинусоиды неопределенна. Полагается, что
она равна погрешности дискретизации параметра -
 д, тогда:
д, тогда:
F(t) =
 д
д
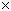 cos
cos t ; F"(t)max =
t ; F"(t)max =
 д
д
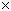
 2 = | f"(t)max | .
2 = | f"(t)max | .
Отсюда: ____________
 =
=
 ( | f"(t)max | ) /
( | f"(t)max | ) /
 д .
д .
Тогда в окончательном виде формула аппрксимирующей косинусоиды примет вид:
___________
F(t)= д
д
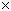 cos{[
cos{[ (|f"(t)|max)/
(|f"(t)|max)/ д ]
д ]
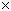 t } .
(2.3)
t } .
(2.3)
Чтобы связать полученную
аппроксимирующую косинусоиду частотой отсчетов необходимо применит понятие стробоскопического
эффекта. Более подробно вопросы, связанные со стробоскопическим эффектом, рассмотрены в ПРИЛОЖЕНИИ 2.
Здесь отметим, что при выполнении равномерных отсчётов с синусоиды, в случае если частота отсчетов
равна удвоенной частоте синусоиды, за счет фазовой неопределенности отсчёты могут случайно попадать
на любые ее значения, включая как экстремумы, так и нули. В связи с этим, при этом возникает 100%
погрешность в отображении синусоиды. Учитывая, что амплитуда апроксимирующей косинусоиды равна
допустимой погрешности измерения параметра, то частота отсчетов равная удвоенной частоте
аппроксимирующей косинусоиды как раз и будет искомой частотой опроса измеряемого параметра, или fд = 2 а.к./2p =
а.к./2p =
 а.к/p .
а.к/p .
Или: ___________
fд = 1/
 | f"(t)max | /
| f"(t)max | / д .
(2.4)
д .
(2.4)
Таким образом, формула определения частоты дискретизации получена. Теперь
необходимо привести ее к виду удобному в практическом использовании.
9. Обычно принято выражать погрешность в виде
приведенной погрешности к максимальной величине диапазона измерений в процентах.
Отсюда: _____________ _____________
fд=10/
 | f"(t)max | /(
| f"(t)max | /( д
д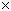 A)
A)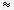 3
3 | f"(t)max | /(
| f"(t)max | /( д
д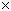 A) ,
(2.5) где fд - частота дискретизации,
A) ,
(2.5) где fд - частота дискретизации,
 д - приведенная
погрешность дискретизации в процентах, A - диапазон измерения.
д - приведенная
погрешность дискретизации в процентах, A - диапазон измерения.
Эта формула уже пригодна к использованию.
Действительно, если известно, например, что высота полета самолета в диапазоне 0 - 10000 м, допустимая
погрешность дискретизации - 0.5% и при максимально допустимой перегрузке по вертикальной оси самолета -
до 5g, то учитывая, что f"(t)max = (Ng - 1) х 9.8 , получим:
__________________
fд = 3 [(5-1)
[(5-1)
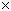 9.8]/(0.5
9.8]/(0.5
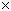 10000)
10000)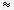 0.3гц.
0.3гц.
10. В ряде практически важных
случаев желательно графическое представление второй производной. Известно [5], что:
_______
k = f"(t)/( 1+[f'(t)]2)3,где k - кривизна функции f(t).
1+[f'(t)]2)3,где k - кривизна функции f(t).
В точке экстремума f'(t) = 0,
следовательно k = f"(t). Так как k = 1/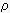 , где
, где
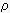 - радиус кривизны, то
- радиус кривизны, то
___________
fд = 3 /
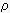 min
min
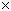
 д
д
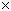 А .
(2.6)
А .
(2.6)
Это второй вариант формулы (2.4).
11. В отдельных случаях получить
вторую производную затруднительно, а в других случаях радиус кривизны меньше допустимой погрешности. В
этих случаях удобнее использовать первую производную функции для определения частоты опросов.
|
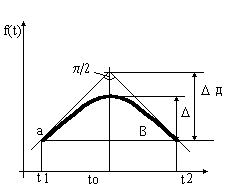
|
|
Рис.2 |
Действительно (Рис.2), если считать
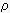
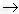 0, в точке t = t0 и масштаб времени выбран таким образом, что угол касательных к
аппроксимирующей косинусоиде в точках ее максимальных первых производных (точках перегиба) -
0, в точке t = t0 и масштаб времени выбран таким образом, что угол касательных к
аппроксимирующей косинусоиде в точках ее максимальных первых производных (точках перегиба) - 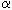 =
=
 /4 , то окрестности точки максимальной
кривизны будут представлять излом функции с углом
/4 , то окрестности точки максимальной
кривизны будут представлять излом функции с углом
 /2. Диапазон от
точки излома до линии (a,b) выбирается равным погрешности дискретизации -
/2. Диапазон от
точки излома до линии (a,b) выбирается равным погрешности дискретизации -
 д, в котором поведение функции может быть любым. В том числе, она может быть и косинусоидой с
таким периодом, что в точках a и b она имеет своими касательными линии максимальной крутизны.
д, в котором поведение функции может быть любым. В том числе, она может быть и косинусоидой с
таким периодом, что в точках a и b она имеет своими касательными линии максимальной крутизны.
Радиус кривизны косинусоиды в точке t0
равен r = (2/ )
) д. Если подставить в
формулу (2.4 ) полученную величину
д. Если подставить в
формулу (2.4 ) полученную величину
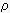 = |f"(t)max|, то
= |f"(t)max|, то
___________
fд = (1/ )
)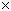 1/
1/
 д
д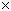 (2/
(2/ )
)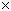
 д , а также
учитывая, что величину погрешности Dд надо также умножить на величину
2/
д , а также
учитывая, что величину погрешности Dд надо также умножить на величину
2/ ,
,
_______
то: fд = (1/ )
)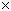 1/
1/
 2 ( 4/
2 ( 4/ 2) = 1/2
2) = 1/2 .
(2.7)
.
(2.7)
Эту формулу можно получить и проще.
Действительно, интервал t1- t2 равен двум полуинтервалам (t1 – t0) и ( t0 - t2) каждый из которых равен
 д. Отсюда t2
- t1 = 2
д. Отсюда t2
- t1 = 2 д и, в свою очередь, fд=1/2
д и, в свою очередь, fд=1/2 .
Но было бы желательно делать вывод из общих позиций. Последний же вывод лишний раз показывает
правильность описанного метода.
.
Но было бы желательно делать вывод из общих позиций. Последний же вывод лишний раз показывает
правильность описанного метода.
Далее, учитывая понятие
приведенной погрешности, получим: fд = 50/ дA. Учитывая, что масштаб
времени t выбран специально для вывода формулы (2.7), и то, что частота опросов меняется линейно с
изменением масштаба времени, а также то, что
дA. Учитывая, что масштаб
времени t выбран специально для вывода формулы (2.7), и то, что частота опросов меняется линейно с
изменением масштаба времени, а также то, что
 x/
x/ t = tg x, можно написать: fд = 50tg(
t = tg x, можно написать: fд = 50tg(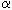 max) /
max) /
 дA, или fд = 50f'(t)max /
дA, или fд = 50f'(t)max /
 дA. (2.8) Полученные формулы эффективны
при
дA. (2.8) Полученные формулы эффективны
при
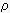
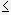
 , в случае
, в случае
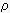 >
>  эти формулы дадут завышенное значение fд. Можно меняя масштаб времени t,
обеспечить выполнение условия
эти формулы дадут завышенное значение fд. Можно меняя масштаб времени t,
обеспечить выполнение условия
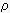
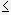
 , при этом формула (2.8) приобретет
вид:
, при этом формула (2.8) приобретет
вид:
fд = М50tg
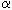 max /
max /
 дA , где М
- масштаб времени.
дA , где М
- масштаб времени.
Вполне резонно можно поставить вопрос о
точности косинусоидальной аппроксимации. Этот вопрос рассмотрен в ПРИЛОЖЕНИИ 3.
12. В заключение раздела приведем
совокупность полученных формул:
fд = (1/ )fс arc cos(1 -
)fс arc cos(1 -
 д).
(2.9)
д).
(2.9)
Эта формула получается решением формулы (П2.1),
где N = fд/fс, а fс частота колебаний синусоидальной функции f(t). При приведенной погрешности она имеет вид:
fд = (f / )arc cos(1-
)arc cos(1- д/100).
Эта формула может применяться к параметрам имеющим явно выраженный колебательный характер. Например,
колебания элементов конструкции летательного аппарата.
д/100).
Эта формула может применяться к параметрам имеющим явно выраженный колебательный характер. Например,
колебания элементов конструкции летательного аппарата.
___________
Формула fд = 3 |f"(t)max| /
|f"(t)max| /
 дA (2.10) применяется к параметрам,
получение величины максимальной второй производной в отношении которых не представляет больших
затруднений.
дA (2.10) применяется к параметрам,
получение величины максимальной второй производной в отношении которых не представляет больших
затруднений.
_____
Формула fд = 3/
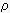
 дA , (2.11)
применяется тогда, когда возможно геометрическое построение зависимости параметра от времени. В
частности, тогда, когда имеется хотя бы одна реализация параметра в его наиболее динамичном виде, (
например записи опробования двигателя ).Кроме того, эта формула может применяться при расчете
количества точек замера по пространственной координате, например количество тензодатчиков по размаху
крыла, При этом строится эпюра механических напряжений и по ее кривизне определяется интервал между
датчиками.
дA , (2.11)
применяется тогда, когда возможно геометрическое построение зависимости параметра от времени. В
частности, тогда, когда имеется хотя бы одна реализация параметра в его наиболее динамичном виде, (
например записи опробования двигателя ).Кроме того, эта формула может применяться при расчете
количества точек замера по пространственной координате, например количество тензодатчиков по размаху
крыла, При этом строится эпюра механических напряжений и по ее кривизне определяется интервал между
датчиками.
Формула fд = 50tg
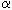 max /
max / дA (2.12)
применяется в отношении параметров имеющих
дA (2.12)
применяется в отношении параметров имеющих
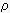 < Dд, и графическое представление которых достаточно просто. Например, отклонение органов
управления летательного аппарата, которое может регистрироваться на земле. Эта формула может также
применяться в случае
< Dд, и графическое представление которых достаточно просто. Например, отклонение органов
управления летательного аппарата, которое может регистрироваться на земле. Эта формула может также
применяться в случае
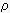 > Dд. В этом
случае применяется коэффициент М по шкале времени и формула приобретает вид: f=M50tg
> Dд. В этом
случае применяется коэффициент М по шкале времени и формула приобретает вид: f=M50tg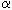 max/
max/ A .
A .
Формула fд = 50f'(t)max
/ дA (2.13) применяется в отношении
параметров, для которых более предпочтительным является использование первой производной. Например,
скорости. Однако нужно иметь в виду, что данная формула может дать завышенное значение частоты опросов.
дA (2.13) применяется в отношении
параметров, для которых более предпочтительным является использование первой производной. Например,
скорости. Однако нужно иметь в виду, что данная формула может дать завышенное значение частоты опросов.
В том случае, если заранее известно, что
зависимость параметра от времени является очень близкой к квадратичной, формула (2.9) даст погрешность в
1,5 раза больше. В большинстве случаев (см. ниже) учитывая, что погрешность дискретизации определяется по
критерию ничтожной погрешности по отношению к погрешности измерения параметра, этим можно пренебречь.
В отдельных случаях может быть применена несколько видоизмененная формула из [6]:
______________
fд = 3,5 |f"(t)max| /
|f"(t)max| /
 дA .
дA .
Описанный метод имеет ряд свойств с точки
зрения восстановления сигнала (интерполяции) и его стохастических характеристик. В следующей главе
рассматриваются эти свойства.
ГЛАВА 3. ИНТЕРПОЛЯЦИЯ И
ЭКСТРАПОЛЯЦИЯ
Задача интерполяции и экстраполяции
неразрывно связана с задачей дискретизации. Интерполяция в явном или неявном виде производится всегда.
В явном виде интерполяция производится в тех случаях, когда параметры необходимые для расчета какой
либо характеристики измеряются с разной частотой, а характеристика вычисляется с частотой большей, чем
частота опросе всех или некоторой части параметров. Кроме того, интерполяция производится в ряде
случаев при графическом представлении параметров или характеристик. При этом интерполяция
производится программно или аппаратно. В неявном виде интерполяция производится в том случае, если
информация регистрируется в табличном виде и интерполяцию производят сознательно или бессознательно
производя оценку значений функции между замерами.
Проблема интерполяции давно привлекала
математическую мысль. История этого вопроса, его анализ и критика рассмотрены в ПРИЛОЖЕНИИ 4. В целом,
известные методы интерполяции можно разделить на три основных группы:
- методы с применением степенных рядов;
- методы с
применением ортогональных функций;
- методы стохастического анализа.
Их анализ (см. ПРИЛОЖЕНИЕ 4) показывает, что в
отношении дискретизации достаточно удобных методов дискретизации нет, что вынуждает нас попытаться
решить эту проблему самостоятельно. Ниже описана методика интерполяции вытекающая из метода
косинусоидальной аппроксимации.
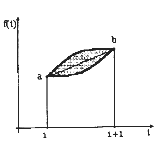
1. Имеются два очередных замера параметра
в моменты времени t1 и t2. (Рис.3 ). Поскольку интервал t2 – t1 определяется
на основе косинусоидальной аппроксимации, то известно, что функция параметра ограничена полупериодами
косинусоиды. Так как величина второй производной в формуле (2.3) берется в виде модуля, то полупериод
косинусоиды имеет или положительный, или отрицательный знак. Очевидно, что область между косинусоидами
есть область вероятного нахождения реального значения параметра.
|
|
|
Рис.3 |
Распределение вероятности значения параметра в этом
интервале симметрично по отношению линии (а – b). Поэтому линия (а - b) является
геометрическим местом точек математического ожидания значений параметра. Вполне естественно, что
интерполирующая линия должна совпадать с линией (а – b), то есть интерполяция должна
быть кусочно-линейной и иметь вид:
f(t) = a + bt, где a = f( ti );
b определяется следующим
образом :
f(t) = f(ti )+bt ; f (ti+1) = f(ti) + bti+1 ; b = [f(ti+1) - f(ti)]/ti+1
. Таким образом, расчетная формула для определения текущего значения f (t) между точками замеров ti и
ti+1 определяется уравнением: f(t) = f(ti) + {[f(ti+1) - f(ti)] / ti+1}t,где ti+1 определяется от начала отсчета, которым принято ti , то есть ti+1 = Т, где Т интервал дискретизации.
Отсюда f(t) = f(ti) + {[f(ti+1) - f(ti)] /T}t.
Преимуществом линейной
интерполяции является простота и удобство ее реализации на ЭВМ. Знаменательно, что, несмотря на
неоднократные попытки применения более сложных методов интерполяции, на практике в основном применяют
линейную интерполяцию.
2. А теперь рассмотрим вопрос в несколько
большей общности. Если положить, что в некоторый момент ti произведен отсчет и получено точное
значение параметра f (ti) , то до следующего отсчета можно ввести одно условие, что измеряемый
параметр не изменится больше , чем на величину заданной погрешности
 .
Действительно, никакая физическая величина не может изменить свое значение мгновенно. Изменение
параметра на
.
Действительно, никакая физическая величина не может изменить свое значение мгновенно. Изменение
параметра на
 сопряжено с некоторым
сопряжено с некоторым
 t. Причем, интервал между отсчетами Т должен быть равным
t. Причем, интервал между отсчетами Т должен быть равным
 t,
поскольку при условии Т>
t,
поскольку при условии Т> t увеличится погрешность выше допустимой, а
при T<
t увеличится погрешность выше допустимой, а
при T< t замеры ti+1 и ti становятся коррелированы а,
следовательно, информационно избыточны. При Т=
t замеры ti+1 и ti становятся коррелированы а,
следовательно, информационно избыточны. При Т=
 t отсчеты становятся
не коррелированы. Неопределенность величины f(t) к точке ti+1 пределами ±
t отсчеты становятся
не коррелированы. Неопределенность величины f(t) к точке ti+1 пределами ± . То есть можно сказать, что при Т =
. То есть можно сказать, что при Т =
 t, отсчеты в пределах ±
t, отсчеты в пределах ± становятся цепью Маркова, или, в более общем понимании, мартингалом.
Естественно, что знание значений f(t) в прошлом ничего не может дать в определении f(t) на
Отсюда станономами выше первой
степени ( то b>i - n), где n = 1,2, . . .), является бессмысленным. В этом и суть
появляющихся ошибок при полиномиальной интерполяции с увеличением степени полинома [7].
становятся цепью Маркова, или, в более общем понимании, мартингалом.
Естественно, что знание значений f(t) в прошлом ничего не может дать в определении f(t) на
Отсюда станономами выше первой
степени ( то b>i - n), где n = 1,2, . . .), является бессмысленным. В этом и суть
появляющихся ошибок при полиномиальной интерполяции с увеличением степени полинома [7].
В данном случае считалось, что значение f(ti+1)
неизвестно, то есть решалась задача экстраполяции. Если же известно f(ti+1), то ясно, что f(t) должна из
известного f(ti) перейти к известному значению f(ti+1). Она может произвести этот переход
равновероятно отклоняясь от прямой линии соединяющей эти точки, что определяет симметричность
распределения вероятности относительно линии f(ti) - f(ti+1) , а, следовательно и выбор этой линии
как интерполирующей. При этом максимальное отклонение этой линии при условии ограничения функции по
второй производной и аналитичности функции будет ограничено полупериодами косинусоиды. Следовательно, рассматривая f(ti) как цепь Маркова, при Т > ti+1 - ti можно
сделать вывод об оптимальности линейной интерполяции.
3. Можно привести и следующие рассуждения.
Исходя из того, что аппроксимирующая косинусоида может быть одной из реализаций исследуемого
параметра при его максимальной, при заданных условиях, динамичности, можно получить
автокорреляционную функцию этого параметра R(t), которая, как известно, будет иметь вид синусоиды.
Очевидно, что значение R(t) = 0 ограничивает область, в которой значения параметра стохастически, а
следовательно и информационно связаны. Поскольку период R(t) равен периоду F(t), можно сделать вывод , что
вне интервала Т любые отсчеты не могут дать дополнительной информации о параметре, а следовательно их
использование в целях интерполяции на интервале Т бессмысленно.
4. Экстраполяция часто применяется в ИИС,
особенно тогда, когда обработка информации производится в реальном масштабе времени, и в частности,
когда ИИС включена в контур управления объектом. Задача экстраполяции представляет по существу задачу
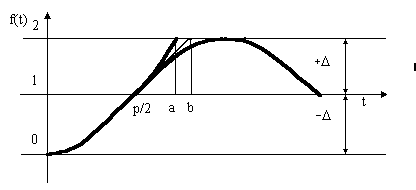
предсказания [8]. Поскольку для определения частоты дискретизации выбирается критерий максимальной
кривизны, то есть максимальной второй производной, то можно полагать, что на интервале от ti до ti+1
( см. Рис.4 ) вторая производная будет постоянной и максимальной, то есть |f"(t)max | =
const.
|
|
|
Рис.4 |
В этом случае f(t) будет представлять собой
параболу f(t) = (at)2 . При f(t) = 1 ( принимается за 0 ), t=
принимается за 0 ), t= /2. Отсюда: (a
/2. Отсюда: (a /2)2=1. Тогда: a2
/2)2=1. Тогда: a2 2=4 ; a=2/p; следовательно f(t)=(2t/
2=4 ; a=2/p; следовательно f(t)=(2t/ )2. При f(t)=2, t=
)2. При f(t)=2, t= /
/ 2 ,
2 ,  /
/ 2-
2- /2»
/2» ´0,208. Поскольку
полупериод косинусоиды (он же интервал отсчетов) равен
´0,208. Поскольку
полупериод косинусоиды (он же интервал отсчетов) равен  , то отношение
, то отношение
 /
/ ´0,208
´0,208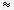 4,8 дает
отношение требуемой частоты дискретизации при экстраполяции по отношению к частоте дискретизации при
интерполяции. Таким образом, частота экстраполяции должна быть выше частоты интерполяции почти в пять
раз. С другой стороны, функция f(t) может быть после точки
4,8 дает
отношение требуемой частоты дискретизации при экстраполяции по отношению к частоте дискретизации при
интерполяции. Таким образом, частота экстраполяции должна быть выше частоты интерполяции почти в пять
раз. С другой стороны, функция f(t) может быть после точки  /2 и
синусоидальной.
/2 и
синусоидальной.
По существу это две крайние возможности.
В условиях неопределенности имеет смысл выбрать нечто среднее, а именно линию касательную к синусоиде
в точке p / 2. Таким образом, мы можем получить точку b, которая делит
интервал дискретизации в p раз. То есть частота экстраполяции будет
примерно в три раза больше частоты интерполяции.
|
|
|
Рис.5 |
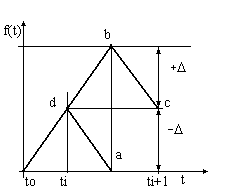
В том случае, когда частота опроса определяется по максимальной первой
производной (Рис.5), f(t) может от точки d перемещаться или к точке b, или к точке а.
Очевидно, что чтобы параметр не вышел за пределы допуска
 необходимо
и достаточно уменьшить величину интервала вдвое, то есть увеличить частоту дискретизации
вдвое. Таким образом, для случая экстраполяции нужно формулы (2.9,2.10,2.11) умножить на 3, а формулы (2.12,2.13) на 2.
необходимо
и достаточно уменьшить величину интервала вдвое, то есть увеличить частоту дискретизации
вдвое. Таким образом, для случая экстраполяции нужно формулы (2.9,2.10,2.11) умножить на 3, а формулы (2.12,2.13) на 2.
ГЛАВА 4. СТОХАСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДИСКРЕТИЗАЦИИ
При синтезе ИИС необходимо метрологическое согласование её
элементов. Это требует исследования стохастических характеристик ее элементов, в том числе и процесса
дискретизации. При этом необходимо иметь в виду, что дискретизация и кусочно-линейная интерполяция
составляют единый процесс преобразования информации, поэтому погрешность дискретизации является
одновременно и погрешностью интерполяции. В этих условиях исследовав стохастические характеристики
дискретизации уже нет необходимости ставить вопрос о стохастических свойствах интерполяции.
Действительно, в моменты отсчетов мы имеем точный замер. Неопределенность появляется за счет
неопределенности информации в промежутке между отсчетами. В этом смысле можно говорить или о точности
интерполяции как способа восстановления информации после дискретизации, или о точности дискретизации
как о процессе преобразования в целом.
1.Ясно, что погрешность дискретизации наибольшая там, где
наибольшая неопределенность информации, а она наибольшая в середине интервала. В этом процессе имеются
две случайные составляющие:
- неопределенность в динамичности параметра в данный момент.
Динамичность может быть максимальна и тогда, когда мы имеем реализацию в виде аппроксимирующей
косинусоиды. И минимальная динамичность, при которой аппроксимирующая синусоида вырождается в прямую
линию. Обычно параметр протекает как-то средне и более-менее близок к нормальному распределению.
- неопределенность в положении отсчетов по отношению к
аппроксимирующей косинусоиде. В этом случае мы имеем арккосинусоидальный закон распределения
погрешности. Определение совместного закона распределения этих двух составляющих довольно сложно,
да и не очень нужно. Учитывая ничтожность [9] влияния погрешности от погрешности на погрешность процесса
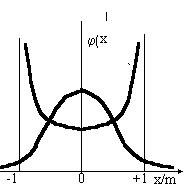
измерения в целом можно считать его и нормальным, однако если посмотреть на Рис.6, можно считать вполне
обоснованным и более точное мнение, что погрешность дискретизации имеет равномерное распределение. В
работе [10] показано, что применение доверительной вероятности Р = 0,997 соответствующей уровню 3 не имеет достаточно оснований, поскольку он соответствует особенностям нормального распределения.
Поскольку это условие не всегда выполняется, то рекомендуются другие критерии. В частности, исходя из
анализа ряда распределений, автор работы [10] приходит к выводу, что для широкого класса законов
распределения самым предпочтительным является Р = 0,95 при
не имеет достаточно оснований, поскольку он соответствует особенностям нормального распределения.
Поскольку это условие не всегда выполняется, то рекомендуются другие критерии. В частности, исходя из
анализа ряда распределений, автор работы [10] приходит к выводу, что для широкого класса законов
распределения самым предпочтительным является Р = 0,95 при
 = 1,65. Это особенно важно при
суммировании погрешностей. В связи с этим, ниже принимается такая рекомендация.
= 1,65. Это особенно важно при
суммировании погрешностей. В связи с этим, ниже принимается такая рекомендация.
|
|
|
Рис.6 |
|
|
|
Рис.7 |
При выборе погрешностей ИИС важно придерживаться системного
подхода. В этом плане элементы ИИС можно распределить на три группы в соответствии со следующими
преобразованиями:
- аналоговые преобразования;
- цифровые преобразования;
- дискретизация.
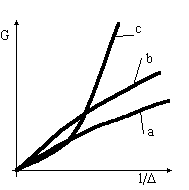
На Рис.7 показана зависимость интегральных затрат на аппаратуру -
G в зависимости от требований к точности этой аппаратуры. Под интегральными затратами понимаются все
виды требуемых затрат на аппаратуру, а именно: веса, габаритов, потребляемой мощности, себестоимости и т.д.
Кривая -a- соответствует цифровым преобразованиям. Действительно, точность цифровых преобразований
зависит от разрядности чисел. Она связана с точностью соотношением:
N=log2(80/2 п), (4.1) где
п), (4.1) где
 п приведенная погрешность измерения.
п приведенная погрешность измерения.
Действительно: N = log2m, где m число уровней разбиения
диапазона измерения в геометрической мере. Но в пределах одного уровня параметр до квантования
определен по равномерному закону ( в силу его неопределенности) с математическим ожиданием посредине
уровня. С учетом Р = 0,95 и
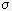 = 1,65 соответствует 0,8. Таким образом
= 1,65 соответствует 0,8. Таким образом
 п
соответствует величине уровня квантования 2
п
соответствует величине уровня квантования 2 п/0,8. Учитывая, что приведенная
погрешность выражена в процентах, диапазон измерений равен 100%, что позволяет получить формулу (4.1).
Очевидно, что при росте точности измерения G будет расти по логарифмическому закону.
п/0,8. Учитывая, что приведенная
погрешность выражена в процентах, диапазон измерений равен 100%, что позволяет получить формулу (4.1).
Очевидно, что при росте точности измерения G будет расти по логарифмическому закону.
Что касается погрешности дискретизации, то она связана с
частотой опроса формулой: fд = К
 ( 1/
( 1/ д), где К - коэффициент
пропорциональности. При использовании первой производной: fд=К(1/
д), где К - коэффициент
пропорциональности. При использовании первой производной: fд=К(1/ д). В общем
случае, можно считать, что зависимость fд (
д). В общем
случае, можно считать, что зависимость fд ( д ) пройдет между линейной
зависимостью и зависимостью пропорциональной корню квадратному - кривая -b- на Рис.7.
д ) пройдет между линейной
зависимостью и зависимостью пропорциональной корню квадратному - кривая -b- на Рис.7.
Обеспечение необходимой точности аналоговыми средствами
требует наибольших затрат. Общеизвестно, что увеличение этих затрат с ростом требуемой точности близко
к степенной зависимости - кривая -c-. Под погрешностью аналоговых преобразований подразумевается как
методические, так и инструментальные погрешности датчиков.
3. При выборе соотношений погрешностей преобразований необходимо
пользоваться принципом ничтожной погрешности. Сущность ее состоит в следующем. Известно, что сложение
погрешностей производится по формуле:
________
 с
=
с
= 
 12 +
12 +
 22.
22.
Полагая, что
 1 = 1, получим:
1 = 1, получим:
______
 с =
с =
 1 +
1 +
 22 .
22 .
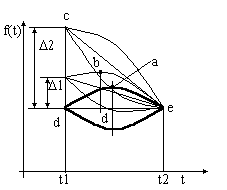
Эта зависимость показана на Рис.8. Очевидно, что учитывая рекомендации [9], можно полагать, что
отклонение заданной погрешности от номинальной до 0,1 её величины практически не меняет степень доверия
к информации. Обычно и определение норм погрешности имеет весьма приближённый, качественный характер.
|
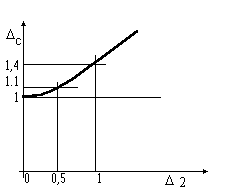
|
|
Рис.8 |
Исходя из этого, можно полагать, что при
 2
меньше или равно 0,5, влиянием её можно пренебречь. Обычно принимают за критерий ничтожной малости 0,3.
2
меньше или равно 0,5, влиянием её можно пренебречь. Обычно принимают за критерий ничтожной малости 0,3.
4. Исходя из вышеизложенного, можно принять такую методологию:
Погрешности квантования при достаточной разрядности АЦП, вычислительных устройств и накопителей
информации можно пренебречь. Действительно, уже при восьми разрядах погрешность квантования
составляет менее 0,1%. Обычно разрядность квантования значительно больше. Погрешность же дискретизации
на основании критерия ничтожной малости можно принимать в три раза меньше чем совокупная методическая
и инструментальная погрешность. В этом случае можно полагать, что процесс дискретизации погрешностей в
процесс измерения вообще не вносит.
ГЛАВА 5. ВЛИЯНИЕ ПОМЕХ НА ДИСКРЕТИЗАЦИЮ
Важным стохастическим свойством дискретизации является влияние
на нее помех. Под помехами обычно подразумевают аномальные измерения и шумы.
1. Шумы имеют частоты находящиеся вне диапазона частот измерений,
в связи с этим воздействие шума на соседние отсчеты некоррелировано. На Рис.9 показано влияние шума на
дискретизацию при условии, что воздействию шумовой помехи подвергнута выборка t1.
|
|
|
|
Рис.9 |
Рис.10 |
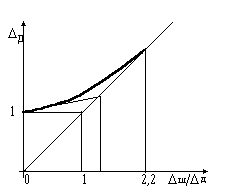
При величине шумовой помехи
 1 точка максимальной погрешности дискретизации перейдет из
точки а, в точку b. При
1 точка максимальной погрешности дискретизации перейдет из
точки а, в точку b. При
 2 - в точку c. Зависимость суммарной погрешности от шумовой помехи
показана на Рис.10. Очевидно, что по критерию ничтожной погрешности, уже при
2 - в точку c. Зависимость суммарной погрешности от шумовой помехи
показана на Рис.10. Очевидно, что по критерию ничтожной погрешности, уже при
 ш < 0,5 его
можно не учитывать, а при
ш < 0,5 его
можно не учитывать, а при
 ш > 2,2, его влияние становится определяющим. Шум, вообще говоря,
действует на обе соседние выборки.
ш > 2,2, его влияние становится определяющим. Шум, вообще говоря,
действует на обе соседние выборки.
|
|
|
Рис.11 |
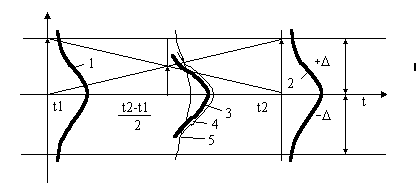
На Рис. 11 показано, что в этом случае, полагая, что шум распределен близко к нормальному закону (хотя это
не так и важно), влияние шума на погрешность уменьшается. Действительно, при величине
 ш<
ш<
 д , Влияние его проявляется в области точки (t2 - t1)/2, как от выборки t1, так и t2. Очевидно при
этом погрешность
д , Влияние его проявляется в области точки (t2 - t1)/2, как от выборки t1, так и t2. Очевидно при
этом погрешность
_______________
 (t1+t2)/2=
(t1+t2)/2=
 (
(  ш1/2)2 + (
ш1/2)2 + ( ш2/2)2
ш2/2)2
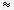 0,7
0,7 ш .
ш .
Таким образом, дискретизация с кусочно-линейной
интерполяцией обладает свойством фильтрации, уменьшая влияние шума в 0,7 раза. При этом шум в 0,7 раза
меньше чем погрешность дискретизации может не учитываться вообще, поскольку влияние его ничтожно. При
амплитуде шума больше 0,7, необходимо увеличение частоты опроса с целью дальнейшего выполнения операций
по фильтрации.
2. Теория фильтрации является важной частью теории
информации. С точки зрения связи этот вопрос рассматривается давно, в том числе и при дискретной связи.
В отношении проблем фильтрации в приложении к информационно-измерительным системам ясности нет до
настоящего времени. Фильтрация есть ни что иное, как сравнение совокупности измерений с t i по t
i + n и их усреднение. Поэтому все фильтры, в общем виде, являются рекурсивными. Отличие их состоит в
количестве прямых и обратных связей. Общая схема такого фильтра показана на Рис.12 [11].Выбор
коэффициентов a0 - an и b0 - bm определяют передаточную функцию фильтра и его порядок.
|
|
|
Рис.12 |
Передаточная функция описывается функциями различного вида, что
позволяет их классифицировать разного рода названиями. Например: фильтр Баттеруорта, синусный фильтр
Баттеруорта, тангенсные фильтры, фильтр Чебышева и т.д. Если в фильтре bi= 0, то такой фильтр
называют нерекурсивным фильтром, имеющим различные разновидности (например ИКО-фильтры ). Число
полюсов или нулей фильтра определяет его порядок, что отражается в названии, например: фильтр
Баттеруорта второго порядка. Реализация того или иного фильтра производится автоматически на ЭВМ по
соответствующим программам.
В целом вопрос фильтрации довольно сложен. Но необходимо
заметить, что сложность таких фильтров тогда проявляется, когда для фильтрации используется большое
число отсчетов. Однако, при определении частот опросов по методу косинусоидальной аппроксимации, как
показано ранее, интервал между отсчетами выбирается такой, что отсчеты вне этого интервала
стохастически не связаны с этим интервалом. Поэтому их использование для фильтрации не имеет основания.
Ведь фильтрация есть использование совокупности отсчетов стохастически взаимосвязанных между собой.
Поэтому для фильтрации необходимо повышать частоту опроса. Анализ материалов реальных измерений
показывает, что характеристики помех таковы, как будет показано далее, что избыточность частоты
отсчетов нужна небольшая (в два - три раза). Поэтому задача фильтрации ограничивается простейшими
случаями. Таким образом, подробный анализ описанных в [12] фильтров, в рамках данной работы, не является
необходимым.
Что касается фильтрации по алгоритмам Калмана-Бъюси [13], то эта
фильтрация разработана для многопараметрических систем и отражает структуру этих систем. В простейшей
постановке задачи, когда имеется один измеряемый параметр и математическая модель объекта неизвестна,
фильтрация по Калману сводится к методу минимума средних квадратов ( методу Гаусса), который в свою
очередь при числе замеров равном двум сводится к определению их среднеарифметического.
Вариантами рекурсивных фильтров являются фильтры основанные на
сплайн-функциях. Алгоритм данного фильтра строится на применении линейного преобразования на базе
подвижного интервала, то есть отфильтрованные значения вычисляются для средней точки интервала. Этот
метод также имеет в виду, что все отсчеты информационно связаны, но, как было показано, отсчеты вне
интервала между отсчетами определенными по методу косинусоидальной аппроксимации с этим интервалом
не связаны. Поэтому для фильтрации необходимо увеличивать число отсчетов. Следовательно, метод на
основе сплайн-функций трансформируется просто к усреднению.
3. Анализ материалов реальных измерений показывает, что шумовые
помехи чаще всего сводятся к двум видам, гауссовский шум и синусоидальные колебания с наложенным
гауссовским шумом. Источником шума первого вида как правило являются тепловые шумы в аналоговых цепях
первичных преобразователей. Источником вторых - вибрации конструктивных элементов объекта.
Как было показано выше, случайная выборка из
синусоиды дает арккосинусоидальное распределение. Наложение не нее гауссовского шума сглаживает
боковые выбросы и распределение вероятности, приближается к равномерному. Как было показано выше,
граничная частота спектра измеряемого параметра априорно определяется как аппроксимирующая
косинусоида. При увеличении частоты дискретизации, в отношении данной косинусоиды, погрешность в её
измерении будет уменьшаться по закону, описанному в ПРИЛОЖЕНИИ 2.
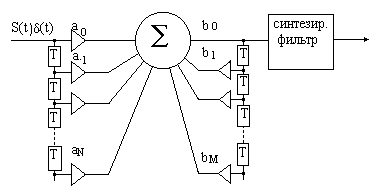
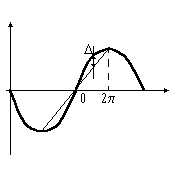
Как было показано ранее, процесс дискретизации, совместно с
интерполяцией, уменьшает помехи примерно в 0,7 раз. Положим, что помеха в виде синусоидального колебания
примыкает к граничной частоте параметра. Максимальная погрешность при дискретизации и дальнейшей
интерполяции для различных N =T/DT имеет вид показанный на Рис.13 , где T период синусоиды,
а DT период дискретизации.
|
|
|
|
Рис.13 |
Рис.14 |
Восстановление функции зависит от фазы отсчетов по отношению к выборкам. Если максимум
синусоидальной функции приходится на средину интервала между отсчетами, то погрешность наибольшая
(100%), если на отсчет, то наименьшая. В последнем случае (Рис.14) погрешность
 x на краю
диапазона равна sinx - 2x/
x на краю
диапазона равна sinx - 2x/ . Определим ее максимальную величину:
. Определим ее максимальную величину:
 'x=(cosx-2/
'x=(cosx-2/ )dx;
)dx;
 'x=0 при cosx=2/
'x=0 при cosx=2/ ; отсюда: x=arccos(2/
; отсюда: x=arccos(2/ ).
).
Следовательно:
 xmax = [(sin arccos(2/
xmax = [(sin arccos(2/ ))-(2/
))-(2/ )arccos(2/
)arccos(2/ )]
=
)]
=
_______
_______
[sin arccsin
 1-(2/p)2 - (2/p)arcsin
1-(2/p)2 - (2/p)arcsin
 1-(2/
1-(2/ )2] =
)2] =
______
______
[ 1-(2/
1-(2/ )2 - (2/p)arcsin
)2 - (2/p)arcsin 1-(
1-( /2)2]
= 0,77 - 0,56 = 0,21, или 21%.
/2)2]
= 0,77 - 0,56 = 0,21, или 21%.
Таким образом, кривая минимума погрешности (21%) пройдет ниже
кривой (100%).
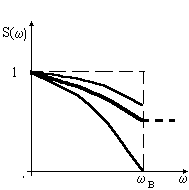
В среднем, учитывая равномерное распределение отсчетов и арккосинусоидальное
распределение выборок по синусоиде, погрешность будет примерно вдвое меньше 100% погрешности. То есть
синусоида на краю диапазона будет искажаться в среднем вдвое. Поэтому АЧХ в зоне полосы пропускания
будет иметь в среднем вид (Рис.15). Этот рисунок имеет в виду амплитуду, соответствующую диапазону
погрешности дискретизации. Частоты же более низкие имеют большую амплитуду. Но, во всяком случае,
погрешность дискретизации не превосходит заданной погрешности.
|
|
|
Рис.15 |
4. Если уровень помех больше допустимого, то можно принять меры по их
фильтрации. Но для этого, как было показано выше необходимо иметь избыточные отсчеты, то есть частоту
опросов нужно увеличивать. Поскольку процесс фильтрации равномерных дискретных отсчетов сводится к их
усреднению, то число их должно увеличиваться кратно исходной частоте дискретизации.
Действительно, как фильтр Калмана при этих условиях сводится к
методу Гаусса, так и рекурсивные методы сводятся к суммированию двух значений с коэффициентом равным -
1/2 и с определением середины интервала. Поэтому, не отвергая всего многообразия методов фильтрации,
можно сделать один вывод, что при наличии двух отсчетов метод фильтрации один, это усреднение.
Предположим, что для обеспечения фильтрации мы
увеличили частоту дискретизации вдвое. При этом, будем увеличивать частоту помехи от wв
(Рис.15). Для начала положим, что она несколько больше частоты wв. Кроме того, учитывая,
что синусоидальные помехи совместно с гауссовским шумом имеют близкое к равномерному распределение
вероятности и могут быть заменены моделью имеющей такое же распределение то далее в качестве модели
принимается колебание в виде треугольного.
|
|
|
Рис.16 |
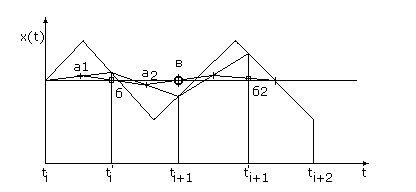
Графически выполнение операции усреднения выражается в соединении соседних точек отсчета прямыми и
определение значения в середине этой прямой (Рис.16) . Далее усредняем полученные точки (а ) и получим
точку (б). Таким образом, мы производим два этапа усреднения, в результате которых всю информацию в
интервале ti-ti+1. Алгебраически эта операция имеет вид: [(а1+а2)/2+(а2+а3)/2]/2,
что равно: а1/4+а2/2+а3/4 , что соответствует рекурсивному фильтру с коэффициентами 1/4 и 1/2. Построим
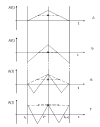
АЧХ такого фильтра ограничившись частотой 4 . На частоте
. На частоте
 в помеха
подавляется в два раза (Рис.17а). На частоте 2
в помеха
подавляется в два раза (Рис.17а). На частоте 2 в помеха подавляется полностью (Рис.17б).
На частоте 3
в помеха подавляется полностью (Рис.17б).
На частоте 3 в снова в два раза, а на частоте 4
в снова в два раза, а на частоте 4 в вообще не
подавляется. Таким образом, АЧХ будет иметь вид (Рис.18). Если необходима большая степень фильтрации,
то нужно еще увеличить частоту отсчетов в два раза. В этом случае АЧХ будет иметь вид (Рис.19)
в вообще не
подавляется. Таким образом, АЧХ будет иметь вид (Рис.18). Если необходима большая степень фильтрации,
то нужно еще увеличить частоту отсчетов в два раза. В этом случае АЧХ будет иметь вид (Рис.19)
|
|
|
Рис.17 |
|

|
|
Рис.18 |
|

|
|
Рис.19 |
|

|
|
Рис.20 |
|
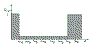
|
|
Рис.21 |
|
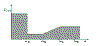
|
|
Рис.22 |
|

|
|
Рис.23 |
|
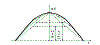
|
|
Рис.24 |
|
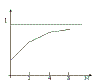
|
|
Рис.25 |
Таким образом, такой фильтр не только подавляет помехи, но и имеет
большую полосу этого подавления. При этом необходимо иметь в виду следующее. Здесь мы рассматриваем
максимальное отклонение шумового сигнала по амплитуде, но это отклонение колеблется периодически, за
счет стробоскопического эффекта, от нуля до максимальной величины. Кроме того, точное положение помехи
неизвестно, поэтому мы можем иметь в виду среднее значение в данной полосе частот. Поэтому, подходя
стохастически к мощности шума можно принять, что АЧХ имеют вид (Рис.20 и 21). То есть первый фильтр
подавляет помеху примерно на 20dB, а второй на 25dB. Учитывая также то, что интерполяция подавляет помеху
еще вдвое, то подавление шумов в первом случае будет примерно на 25dB, а во втором на 30dB, что в практике
измерений вполне достаточно. Что касается более высоких частот шумов, то при их фильтрации их можно
принять с нормальным законом распределения, как гауссовский шум.
____
При этом
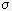 ф =
ф =

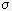 ш2/N где N число
отсчетов используемых для фильтрации. При
ш2/N где N число
отсчетов используемых для фильтрации. При
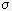 ф/
ф/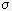 ш = 1/
ш = 1/ N
., если принять
N
., если принять
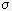 ш = 1 , то
ш = 1 , то
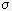 ф = 1/
ф = 1/ N . То есть, при N=2 ,
N . То есть, при N=2 ,
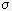 ф=0,7, а при N=4 ,
ф=0,7, а при N=4 ,
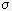 ф=0,25. Учитывая фильтрующие свойства
интерполяции: при N=2,
ф=0,25. Учитывая фильтрующие свойства
интерполяции: при N=2,
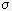 ф=0,35 ; приN=4
ф=0,35 ; приN=4
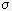 ф=0,25.
ф=0,25.
С учетом этого АЧХ фильтров будут иметь вид (Рис. 22 и 23). Необходимо
иметь в виду следующее. Во-первых, рассматриваемые нами модели несколько искусственны. Поэтому в
низкочастотных синусоидально-подобных шумах присутствуют и высокочастотные помехи. Во-вторых,
эффективность фильтрации синусоиды при увеличении числа выборок растет все медленнее (см. Рис.24) и
подчиняется зависимости Рис.25. Поэтому повышение частот опросов для фильтрации N > 4 не имеет смысла.
Таким образом, процесс фильтрации требует увеличения частот опросов, но алгоритмы расчёта несложные и
достаточно эффективные.
2. Теперь рассмотри вопросы, связанные с аномальными
измерениями. Аномальные измерения могут иметь различные физические причины. К ним могут относиться
дефекты ленты магнитных накопителей, сбои в цифровых линиях передачи, броски питания датчиков, дребезг
контактов и т.д. Однако в информационном плане все они одинаковы. Когда мы смотрим на аномальное
измерение, то можем сказать одно - “ этого не может быть, потому что не может быть никогда”. Проблема
возникает тогда, когда ставится вопрос как определить, может это быть или нет. Очевидно, что ответить на
этот вопрос можно только тогда, когда априорно известна динамика регистрируемого процесса. Например,
если мы видим, что идет запись высоты летательного аппарата равная 5000м и вдруг. через 0,1с. появилась
отметка 200м, то вряд ли кто либо усомнится, что налицо типичное аномальное измерение. Но когда появилась
отметка 5020м, то уже трудно отнести его к аномальному измерению. Нужен критерий достаточно надежный и
простой в реализации в виде вычислительного алгоритма для определения аномального измерения.
Существуют различные алгоритмы ликвидации аномальных измерений.
Здесь мы рассмотрим один из возможных методов, который может быть полезен когда при подготовке ИИС
известна динамика процесса на основе которой, а также при заданной точности измерений, определяется
частота дискретизации измеряемого параметра. В том случае, если частота опроса параметра
определяется на основе теории аппрксимирующей косинусоиды, можно утверждать, что при очередном замере
параметр не может отклониться от предыдущего более чем на 3 .
.
Действительно, в этом случае речь идет об экстраполяции,
поскольку очередной замер нам апосториорно не известен. Мы можем только предполагать его значение.
Поэтому, используя формулу для случая экстраполяции и учитывая, что запись производится для случая
интерполяции, мы считаем, что параметр может измениться на величину не более 3D. В случае,
если частота дискретизации вообще определялась на случай экстаполяции, то в качестве критерия нужно
брать величину  .
.
Что делать с аномальным измерением? Естественно, если оно
аномальное, то это и вовсе не измерение. Можно считать, что его и вовсе не было. Если его необходимо
восстановить, то необходимо взять очередной отсчет и путем интерполяции определить пропущенный.
Естественно, хотим мы этого или нет, но информация для нас потеряна, поэтому погрешность на интервале
пропущенного аномального измерения будет больше заданной. Но вероятность этого небольшая и с ней можно
мириться. Далее, несмотря на то, что мы определяем частоту опросов, точно она не выдерживается по ряду
причин системного характера, например, за счет кратности частот опросов по разным параметрам. Поэтому
часто реальная частота опросов превышает расчетную. Кроме того, точно знать динамику измеряемых
параметров вряд ли возможно, поэтому даже самый компетентный специалист завысит значения
характеристик динамичности измеряемых параметров. И, наконец, учитывая, что параметр редко выходит на
предел динамичности можно в качестве критерия брать не 3 , а 2
, а 2 . В этом
случае погрешность определения аномального измерения и погрешность его восстановления согласуются
почти полностью.
. В этом
случае погрешность определения аномального измерения и погрешность его восстановления согласуются
почти полностью.
Аномальные измерения относятся к тому случаю, когда действия,
которые необходимо предпринять, имеют логические основания и особых исследований с применением
разнообразного и сложного математического аппарата просто не требуется. В этом вопросе возможны два
методических подхода. Первый соответствует тому случаю, когда информация поступает к нам по мере её
возникновения. Мы получаем очередное значение измеряемого параметра, и что будет дальше, не знаем.
Второй случай - когда вся информация или хотя бы часть её после последнего аномального измерения нам
известна. На основе этих подходов могут разрабатываться и различные алгоритмы.
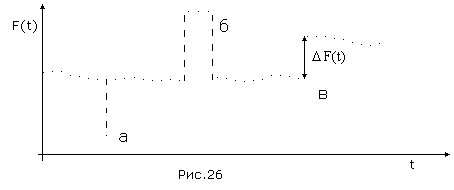 Аномальные
измерения могут следовать в виде единичных измерений (Рис.26а), пачек или пакетов (б), или в виде разрывов
в измерении параметра (в). Первый может быть связан, например, со сбоями в цифровой аппаратуре, второй с
нарушение контактов в потенциометрических датчиках или пропадание напряжения питания, третий,
например, со склейкой различных участков магнитной ленты регистраторов. Выбор решения в таких случаях
требует адаптивного подхода, который в наибольшей степени свойственен логике человеческого мышления.
Аномальные
измерения могут следовать в виде единичных измерений (Рис.26а), пачек или пакетов (б), или в виде разрывов
в измерении параметра (в). Первый может быть связан, например, со сбоями в цифровой аппаратуре, второй с
нарушение контактов в потенциометрических датчиках или пропадание напряжения питания, третий,
например, со склейкой различных участков магнитной ленты регистраторов. Выбор решения в таких случаях
требует адаптивного подхода, который в наибольшей степени свойственен логике человеческого мышления.
Рассмотрим этот вопрос с точки зрения первого методического
подхода. Априорно мы имеем критерий обнаружения 3 . Поэтому, чтобы обнаружить аномальное
измерение, мы производим с каждым полученным измерением операцию сравнения (Рис.27)
. Поэтому, чтобы обнаружить аномальное
измерение, мы производим с каждым полученным измерением операцию сравнения (Рис.27)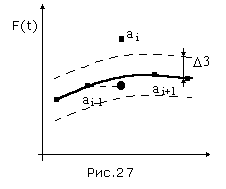 :
:
если | ai – ai+1 | больше 3 , это соответствует 1, если | ai – ai+1
| меньше или равно 3
, это соответствует 1, если | ai – ai+1
| меньше или равно 3 , это соответствует 0 В случае если решение равно 1, то мы
имеем аномальное измерение. Мы потеряли информацию. Ставится задача ее восстановить. При этом можно
принять два решения основывающихся на экстраполяционном и интерполяционном подходе. Выбор того или
иного решения определяется в каждом конкретном случае исходя из двух соображений. С одной стороны,
экстраполяционный подход прост. Просто аi мы принимаем равным ai+1. Однако его погрешность
больше. Интерполяционный подход, при котором ai определяется по формуле: ai=(ai+1 + ai-1
)/2 дает погрешность 1,5
, это соответствует 0 В случае если решение равно 1, то мы
имеем аномальное измерение. Мы потеряли информацию. Ставится задача ее восстановить. При этом можно
принять два решения основывающихся на экстраполяционном и интерполяционном подходе. Выбор того или
иного решения определяется в каждом конкретном случае исходя из двух соображений. С одной стороны,
экстраполяционный подход прост. Просто аi мы принимаем равным ai+1. Однако его погрешность
больше. Интерполяционный подход, при котором ai определяется по формуле: ai=(ai+1 + ai-1
)/2 дает погрешность 1,5 , то есть в два раза меньше, но имеет более сложный алгоритм решения,
а, следовательно, больше время на обработку и больший объем памяти. Однако, имея в виду, что частота
опросов определяется по максимальному критерию погрешности, а расчет измерительной системы в целом, (включая
и стохастические характеристики измеряемого параметра) по среднеквадратическому критерию, есть
основания полагать, что в среднем погрешность экстраполяционного метода сравнима с погрешностью интерполяционного.
Поэтому, есть основания выбрать экстраполяционный метод как основной, учитывая, тем не менее,
возможность применения интерполяционного метода.
, то есть в два раза меньше, но имеет более сложный алгоритм решения,
а, следовательно, больше время на обработку и больший объем памяти. Однако, имея в виду, что частота
опросов определяется по максимальному критерию погрешности, а расчет измерительной системы в целом, (включая
и стохастические характеристики измеряемого параметра) по среднеквадратическому критерию, есть
основания полагать, что в среднем погрешность экстраполяционного метода сравнима с погрешностью интерполяционного.
Поэтому, есть основания выбрать экстраполяционный метод как основной, учитывая, тем не менее,
возможность применения интерполяционного метода.
Теперь перейдём к случаю (б). Очевидно, что интервал между истинными отсчетами ai-1 и ai+1
вдвое больше чем между ai-1 и ai . Поэтому вполне возможно, что за период 2 t ,
параметр отклонится на величину 2´3
t ,
параметр отклонится на величину 2´3 = 6
= 6 . Таким образом,
после первого аномального измерения, мы должны критерий обнаружения аномального измерения увеличить
вдвое. Для следующих аномальных измерений мы поступаем также до тех пор, пока мы не получим нормальное
измерение, после чего веси интервал интерполируем. Экстраполяцией здесь мы не обойдемся, поскольку
будет слишком большая погрешность.
. Таким образом,
после первого аномального измерения, мы должны критерий обнаружения аномального измерения увеличить
вдвое. Для следующих аномальных измерений мы поступаем также до тех пор, пока мы не получим нормальное
измерение, после чего веси интервал интерполируем. Экстраполяцией здесь мы не обойдемся, поскольку
будет слишком большая погрешность.
Число точек при восстановлении в случае (в),Рис.26, будет равно
 a/3
a/3 д.
Например, если разрыв
д.
Например, если разрыв
 а равен 50% диапазона и
а равен 50% диапазона и
 д = 1%, то N = 50/3 или примерно
равно 15 точек. Характер восстановления по описанному методу будет иметь вид (Рис.28).
д = 1%, то N = 50/3 или примерно
равно 15 точек. Характер восстановления по описанному методу будет иметь вид (Рис.28). 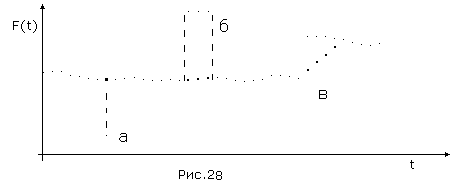 Очевидно, что этот метод, будучи довольно простым, имеет тот недостаток, что теряется информация в
случае разрывов функции. Попытаемся устранить этот недостаток. Чтобы восстановить функцию после ее
последующего анализа необходимо запоминание её предыдущих значений. Положим, что мы имеем такую память.
Тут могут быть два случая. Во-первых, аномальное измерение представленное рядом выборок, число которых,
тем не менее, меньше чем позволяют динамические характеристики объекта. То есть после последнего
аномального отсчета появляется истинный отсчет, который по отношению к аномальному выглядит как
аномальное измерение. В этом случае каждое очередное измерение проверяется по критерию аномальности,
Когда наступит скачек, все предыдущие аномальные измерения отбрасываются и заменяются линейной
интерполяцией. Если через заданное число измерений нового скачка не наступает, то считается, что это
разрыв функции и все предыдущие аномальные измерения считаются верными и передаются на обработку.
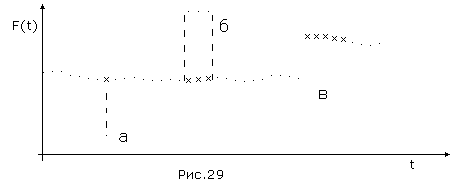
Восстановленная функция при этом будет иметь вид (Рис.29). Однако, как отмечалось, в этом случае
необходима большая оперативная память, а также необходима задержка на обработку, которая может быть
недопустима в случае, если обработка информации должна производится в реальном масштабе времени.
Очевидно, что этот метод, будучи довольно простым, имеет тот недостаток, что теряется информация в
случае разрывов функции. Попытаемся устранить этот недостаток. Чтобы восстановить функцию после ее
последующего анализа необходимо запоминание её предыдущих значений. Положим, что мы имеем такую память.
Тут могут быть два случая. Во-первых, аномальное измерение представленное рядом выборок, число которых,
тем не менее, меньше чем позволяют динамические характеристики объекта. То есть после последнего
аномального отсчета появляется истинный отсчет, который по отношению к аномальному выглядит как
аномальное измерение. В этом случае каждое очередное измерение проверяется по критерию аномальности,
Когда наступит скачек, все предыдущие аномальные измерения отбрасываются и заменяются линейной
интерполяцией. Если через заданное число измерений нового скачка не наступает, то считается, что это
разрыв функции и все предыдущие аномальные измерения считаются верными и передаются на обработку.
Восстановленная функция при этом будет иметь вид (Рис.29). Однако, как отмечалось, в этом случае
необходима большая оперативная память, а также необходима задержка на обработку, которая может быть
недопустима в случае, если обработка информации должна производится в реальном масштабе времени.
|
|
ГЛАВА 4. ПРОДОЛЖЕНИЕ. ФИЛЬТРАЦИЯ
Всё вышеизложенное касается случая, кода параметр
без шумов. Если он имеет шумовую помеху, то необходима фильтрация. Очевидно, что аномальные измерения
должна быть убраны до фильтрации, иначе они могут быть сглажены до такой степени, что уже не будут иметь
вид аномального измерения, но искажение в информацию внесут недопустимое.
Во всём этом вопросе остается одна неясность. Если
число аномальных измерений в пакете велико, то при их восстановлении методом интерполяции
действительные значения параметра на интерполирующем отрезке могут быть весьма большими и
значительно больше погрешности дискретизации. Вполне естественно, что их использование может быть
вообще нецелесообразным. Поэтому тут могут быть три решения:
- аномальные измерения вообще отбрасывать без восстановления;
- допускать восстановление аномальных измерений методом линейной интерполяции в ограниченном числе;
- допускать восстановление неограниченного числа аномальных измерений.
Нетрудно заметить, что описанный алгоритм обладает и фильтрующим
свойством. Действительно, положим, что имеется параметр, искаженный шумом большой амплитуды (Рис.30). 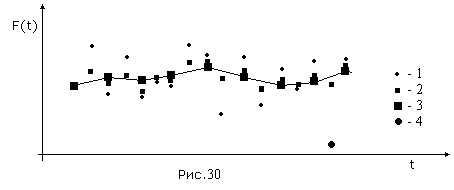 Имеем критерий -
Имеем критерий -
 д. Причем, если данное измерение выходит за пределы Dд, заменяем его значением: ai+1 =ai+
д. Причем, если данное измерение выходит за пределы Dд, заменяем его значением: ai+1 =ai+ . Восстановленные точки будут
иметь вид (точки - 2 на Рис.30). Очевидно, что шум резко уменьшается. Если имеется избыточность частоты
опроса, то можно применить фильтрацию описанную выше. Вновь полученные точки - (3). Из рисунка наглядно
видно, что параметр отфильтрован. При этом убираются и одиночные аномальные измерения (точка - 4).
Преимущества данного метода заключаются в том, что как фильтрация, так и удаление аномальных измерений
производится в одном алгоритме. Недостаток здесь тот, что в случае пачки аномальных измерений или
разрыва функции этот алгоритм становится менее эффективным. Действительно, этот алгоритм не что иное,
как следящее устройство, которое обладает инерционностью. Отслеживая точку аномальных измерений, он
отклоняется от истинного значения параметра. После окончания пачки фильтр довольно медленно
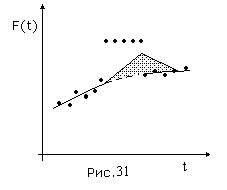
возвращается к математическому ожиданию параметра (Рис.31). В результате получается большая ошибка в
низкочастотной области, которую никак устранить не удаётся. Выход, наверное, состоит в том, что на
случай аномальных измерений, число которых больше m (например - 3) фильтр выключается до их исчезновения.
. Восстановленные точки будут
иметь вид (точки - 2 на Рис.30). Очевидно, что шум резко уменьшается. Если имеется избыточность частоты
опроса, то можно применить фильтрацию описанную выше. Вновь полученные точки - (3). Из рисунка наглядно
видно, что параметр отфильтрован. При этом убираются и одиночные аномальные измерения (точка - 4).
Преимущества данного метода заключаются в том, что как фильтрация, так и удаление аномальных измерений
производится в одном алгоритме. Недостаток здесь тот, что в случае пачки аномальных измерений или
разрыва функции этот алгоритм становится менее эффективным. Действительно, этот алгоритм не что иное,
как следящее устройство, которое обладает инерционностью. Отслеживая точку аномальных измерений, он
отклоняется от истинного значения параметра. После окончания пачки фильтр довольно медленно
возвращается к математическому ожиданию параметра (Рис.31). В результате получается большая ошибка в
низкочастотной области, которую никак устранить не удаётся. Выход, наверное, состоит в том, что на
случай аномальных измерений, число которых больше m (например - 3) фильтр выключается до их исчезновения.
 Таким
образом, в целом алгоритм фильтрации и удаления аномальных измерений может выполняться как одно целое
в виде отдельных блоков, комбинация которых и выбор критериев могут быть различными. Поскольку
переработка алгоритма для каждого случая весьма трудоёмка, то имеет смысл в начале алгоритма иметь
слово описывающее состояние его. В этом случае могут быть идентификаторы, определяющие наличие тех, или
иных критериев, Эти слова могут храниться в самой программе и вызов их может определяться
идентификаторами параметра.
Таким
образом, в целом алгоритм фильтрации и удаления аномальных измерений может выполняться как одно целое
в виде отдельных блоков, комбинация которых и выбор критериев могут быть различными. Поскольку
переработка алгоритма для каждого случая весьма трудоёмка, то имеет смысл в начале алгоритма иметь
слово описывающее состояние его. В этом случае могут быть идентификаторы, определяющие наличие тех, или
иных критериев, Эти слова могут храниться в самой программе и вызов их может определяться
идентификаторами параметра.
3. Аналогично пакету аномальных измерений может
возникнуть и последовательность однополярной выборки шумовой помехи. Очевидно, что при действии
вышеописанного фильтра действие однополярных выборок порождает тот же эффект, что и аномальные
измерения (Рис.31). Здесь появляется возможность ошибки, которая по динамическим характеристикам
подобна измеряемому параметру и поэтому в дальнейшем неустранима.
Понятно, что узкополосный шум, находящийся близко к
области частот измеряемого параметра, будет порождать знакопериодическую последовательность опросов
(Рис.32). При этом эффективность фильтра можно увеличить, уменьшая
 фильтра, но не до такой
степени, что бы это повлияло на точность восстановления параметра. При этом следует, что кратность
однополярных выборок пропорциональна отношению fф/fд. Например, при fф/fд = 4, мы
можем иметь по 4 однополярной выборки. При этом фильтрация усреднения и фильтрация следящего алгоритма
независимы, что позволяет резко повысить эффективность фильтрации, при котором амплитуда шума в
принципе ограничена. Но с ростом амплитуды шума возрастает и амплитуда его высокочастотных
составляющих, следовательно, и вероятность пакетов однополярных выборок, а, следовательно, и ошибки
измерения. Но при этом эффективность фильтра очень высокая.
фильтра, но не до такой
степени, что бы это повлияло на точность восстановления параметра. При этом следует, что кратность
однополярных выборок пропорциональна отношению fф/fд. Например, при fф/fд = 4, мы
можем иметь по 4 однополярной выборки. При этом фильтрация усреднения и фильтрация следящего алгоритма
независимы, что позволяет резко повысить эффективность фильтрации, при котором амплитуда шума в
принципе ограничена. Но с ростом амплитуды шума возрастает и амплитуда его высокочастотных
составляющих, следовательно, и вероятность пакетов однополярных выборок, а, следовательно, и ошибки
измерения. Но при этом эффективность фильтра очень высокая. 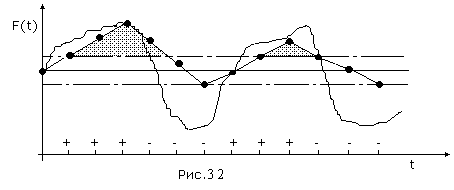
При наличии помех большой амплитуды и частоты, вероятность
нахождения выборок в зоне
 мала и может не учитываться. В этом случае, каждая выборка
будет иметь значения или +
мала и может не учитываться. В этом случае, каждая выборка
будет иметь значения или + , или -
, или - . Такая модель позволяет считать
отдельные выборки независимыми. Модель такого случая может быть представлена в виде бросания монеты.
Построим такую реализацию (Табл.1), Таблица построена в два сеанса опытов по 100 бросков. Определим
распределение кратности (Рис.33) на 200 бросков. Поскольку речь идет об однополярных измерениях, то две
ветви Рис.33 можно усреднить, считая их за 400 бросков.
. Такая модель позволяет считать
отдельные выборки независимыми. Модель такого случая может быть представлена в виде бросания монеты.
Построим такую реализацию (Табл.1), Таблица построена в два сеанса опытов по 100 бросков. Определим
распределение кратности (Рис.33) на 200 бросков. Поскольку речь идет об однополярных измерениях, то две
ветви Рис.33 можно усреднить, считая их за 400 бросков.
|

|
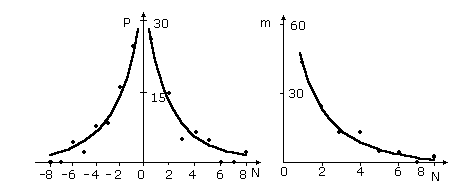
|
|
Табл.1 |
Рис.33
Рис.34 |
Вероятность появления пачки измерений определяются совместно с
вероятностью событий имеющих вероятность 0,5. Поэтому: Р = (0,5)n. Соответственно: Р1 = 1/2, Р2 = 1/4, Р3 =1/8,
Р4 = 1/16, Р5 = 1/32, Р6 = 1/64, Р7 = 1/128, Р8 = 1/256. Такая идеальная кривая показана на Рис. 34. Отсюда, вероятность
пакетов однополярных выборок позволяет определить вероятность ошибки. Определим ее на квантиле 0,95:
Функция f(P) =1/2n, P[x<0,95] = ?
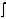 f(P)dP =
f(P)dP =
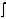 (1/2n) | при n
(1/2n) | при n
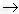
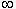 | = 1.
| = 1.
Имеем:
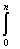 (1/2n) dn =
(1/2n) dn = 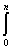 2-ndn =
2-ndn = 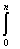 e-n ln2dn = -1/ln2 + 2-n/ln2;
e-n ln2dn = -1/ln2 + 2-n/ln2;
при n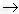
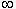 ,
,
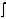 0 = 1/(-ln2), но при этом Р = 1, отсюда 0,95
0 = 1/(-ln2), но при этом Р = 1, отсюда 0,95  0,95 × 1/ln2.
0,95 × 1/ln2.
Следовательно: 1/ln2 - 2-n/ln2 = 0,95 /ln2
или 2-n = 1 - 0,95 = 0,05,то есть 2n = 20.
Отсюда n = 4,3
 4. Таким образом, число в пакете
превышающее 4 нас могут не интересовать, так как вероятность такого события достаточно мала. Описанный
выше подход базируется на некоторой идеализации. В реальной ситуации шумы часто имеют периодический
характер. Это приводит к тому, что распределение Рис.34 несколько искажается. Причем это приводит к тому,
что возрастает вероятность отсчетов меньшей кратности.
4. Таким образом, число в пакете
превышающее 4 нас могут не интересовать, так как вероятность такого события достаточно мала. Описанный
выше подход базируется на некоторой идеализации. В реальной ситуации шумы часто имеют периодический
характер. Это приводит к тому, что распределение Рис.34 несколько искажается. Причем это приводит к тому,
что возрастает вероятность отсчетов меньшей кратности.
Далее, мы рассмотрели процесс фильтрации с D равной
длине шага в относительных величинах. Теперь необходимо учесть, что частоты опросов берутся выше fд
в 4 раза. При этом погрешность дискретизации уменьшается в квадрате, то есть в 16 раз, поэтому D
следующего фильтра может быть в 16 раз меньше. Благодаря этому длина пакета может быть в 16 раз больше. Это
позволяет здесь возможностями кратных помех пренебречь до 16×4 = 64 на интервал дискретизации. Но при
этом необходимо учитывать то, что погрешность дискретизации с увеличением интервала дискретизации
увеличивается квадратично, а погрешность фильтра линейно. Поэтому, сохраняя D фильтра
постоянной необходимо брать её в N раз меньше погрешности дискретизации, где N = fф/ fд .
Поэтому при длине пакета равном N, погрешность не превысит погрешности дискретизации. В частности, при N
= 4, вероятность пакетов пренебрежимо мала. Кроме того, дальнейшая фильтрация, а также свойство
подавления помех при дискретизации делают фильтр в целом достаточно эффективным.
4. Характеристики фильтра можно улучшить. Действительно, пакет
однополярных выборок, чем длиннее, тем менее вероятен. Очевидно, что чем длиннее пакет, тем более
становится вероятным появление выборки другой полярности. Обычно считается, что каждая из независимых
выборок вероятность имеет независимую. Это верно при том условии, когда значениями предыдущих выборок
мы пренебрегаем. Но коль скоро мы имеем возможность запоминать и анализировать предыдущие выборки, то у
нас и имеется возможность предполагать значения последующих. Для иллюстрации этого не столь
известного явления, промоделируем игру, используя Таблицу 2.
|
|
|
Табл.2 |
Суть игры в следующем. Предположим, что мы бросаем монету. Если
полагать, что появление решки (0) и орла (1) равновероятно, то есть смысл считать выигрышем “1” а
проигрышем “0” , выразив это функцией U = (±1). При этом вводим некоторое число ставку “С” . В случае
выигрыша, количественно он выражается произведением U×C. Причем рассмотрим две стратегии.
- Первая - поскольку U равновероятно, то можно ввести ставку в виде постоянного числа и ее не менять -
например, U = 1;
- Вторая - вероятность данной выборки
зависит от предыдущей, причем после, например U = +1 должно выпасть U = - 1 , поэтому ставка по знаку обратная
предыдущему значению U . Мало того, чем длиннее пакет однозначных выборок U , тем больше ставка ожидаемой
выборки. Количественно мы её определяем по формуле С = 2(n - 1) , где n - длина предыдущего пакета. Игру
будем считать законченной при выполнении заранее заданного числа опытов, например - 50. Чем больше, тем
лучше, но уже при N = 10 тенденция начинает вполне просматриваться. Закончив игру, сравниваем результаты
обеих стратегий. Выигрывает та стратегия, у которой сумма выигрыша будет больше. Количественно
результат определяется как разность выигрышей.
Итак, проведя 50 бросков монеты, заполним таблицу (Табл.2). В
результате получено следующее:
Выигрыш первой стратегии - В1 = 6;
Выигрыш второй стратегии - В2 = 24.
Общий выигрыш второй стратегии -
18 очков.
Изобразим процесс графически (рис.35). Что касается первой стратегии, то понятно, что общая
сумма должна лишь колебаться возле нуля, поскольку число выборок обеих знаков, с увеличением N, должно
стремиться к тому, что бы быть одинаковым. В этом и смысл того, что вероятности событий в данном опыте
равновероятны и равны 1/2 . Что касается второй стратегии, то на рисунке видно, что имеется тенденция к
росту выигрыша. Причём темп этого роста равен N/ В2 и при росте N до бесконечности, стремится к 2 . Отсюда
выигрыш стремится к Р×N, или в данном случае - N/2.
|

|
|
Рис.35 |
Суть вопроса состоит в том, что в теории вероятности считается, что события следующие друг за другом
во времени несовместны. То есть, сколько бы мы не бросали монету, перед очередным броском мы полагаем,
что вероятность того, что выпадет орёл, равна 0,5. И это правильно. Но с другой стороны, если мы обладаем
памятью и последовательно бросая монеты запоминаем результат, то становится, вообще говоря, все равно,
бросили ли мы сразу десять монет, последовательно каждую из монет или десять раз одну и туже монету.
Результаты будут почти одинаковы, а при стремлении числа опытов к бесконечности, разность в
результатах будет стремиться к нулю.
Исходя из этого, если мы бросали монету и у нас десять раз подряд
выпадет решка, то нас это начнёт удивлять, и мы подумаем, что пора, наверное, выпасть и орлу. И если уж
ставить ставки, то любой нормальный человек поставит на орла. Конечно, можно и проиграть, но вероятность
этого небольшая. Она равна 1/11. А вероятность выигрыша - 10/11. То есть мы полагаем, что в очередном броске
вероятность выпадения решки равна 1/11, а выпадения орла - 10/11. И это противоречие с понятием классической
теории вероятности объясняется только тем, что своей памятью мы объединяем прошлые опыты-броски в один
эксперимент и несовместные события становятся при этих условиях совместными.
Этот метод известен с XVII века и называется
"мартингейл". Изобретён был игроками в азартные игры. Сейчас широко применяется
при игре на биржах.
Мы также можем разработать алгоритм, который, запоминая
предыдущие аномальные отсчеты, сможет более быстро после окончания пакета аномальных измерений
перейти к нормальным. Для этого мы можем ввести условие, что измерение признаётся нормальным, если
его значение попадает в области допустимой погрешности, которая определяется по формуле
 ×2(n-1)
где n равно числу предыдущих аномальных измерений в пачке. Характер процесса показан на Рис.36.
×2(n-1)
где n равно числу предыдущих аномальных измерений в пачке. Характер процесса показан на Рис.36.
|

|
|
Рис.36 |
Следящий фильтр под действием пакета однополярной ошибки
накапливает ошибку, отслеживая аномальные измерения. Когда пачка оканчивается, он возвращается к
нормальным измерениям (зона Х). Если же погрешность следящего фильтра увеличивается, то при окончании
пачки аномальных измерений ограниченный по динамичности измеряемый параметр окажется в зоне
допустимых значений и захватывается следящим фильтром. При этом энергия помехи от аномальных
измерений существенно уменьшается и делает погрешность от воздействия аномальных измерений более
приемлемой.
5. Таким образом, нами рассмотрена совокупность методов борьбы с
помехами различной природы. Эти методы могу быть объединены в одном вычислительном алгоритме, пример
которого мы ниже рассмотрим.
|
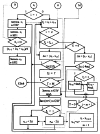
|
|
Рис.37 |
Исходными данными для алгоритма являются погрешность
дискретизации  и число аномальных измерений в пачке М, больше которого вырабатывается
сигнал “Сбой”. Кроме того, задается число N определяемое объёмом буферной памяти №1 (БП1). Эта память
необходима для обработки информации следящим фильтром и объём её определяется числом допустимых
аномальных измерений в одном пакете. То есть ориентировочно N может приниматься равной М.
и число аномальных измерений в пачке М, больше которого вырабатывается
сигнал “Сбой”. Кроме того, задается число N определяемое объёмом буферной памяти №1 (БП1). Эта память
необходима для обработки информации следящим фильтром и объём её определяется числом допустимых
аномальных измерений в одном пакете. То есть ориентировочно N может приниматься равной М.
Условные обозначения в алгоритме:
xi - очередное измерение;
i - номер очередного измерения;
j - номер аномального измерения;
m - суммарное число аномальных измерений;
 x - модуль разности
между очередным и аномальным измерением;
x - модуль разности
между очередным и аномальным измерением;
 -
функция равная “1” если xi > xi-1 и “0” если xi < xi-1 .
-
функция равная “1” если xi > xi-1 и “0” если xi < xi-1 .
В зависимости от ситуации, время для решения алгоритма может быть
разным и достигает максимума при Т =
 t ´ M, где Dt интервал
между измерениями. Кроме того, обработка информации производится по нескольким каналам и, наконец, для
ускорения ввода информации в ЭВМ при полной обработке необходимо уплотнение информации в виде файлов
определенной величины. В силу этого запись информации после фильтрации должна производится в
двухстраничное буферное ЗУ, в котором сначала информация от фильтра записывается на одну страницу, а
ввод в ЭВМ с другой. Затем страницы меняются.
t ´ M, где Dt интервал
между измерениями. Кроме того, обработка информации производится по нескольким каналам и, наконец, для
ускорения ввода информации в ЭВМ при полной обработке необходимо уплотнение информации в виде файлов
определенной величины. В силу этого запись информации после фильтрации должна производится в
двухстраничное буферное ЗУ, в котором сначала информация от фильтра записывается на одну страницу, а
ввод в ЭВМ с другой. Затем страницы меняются.
Итак, алгоритм работает следующим образом:
При получении первого измерения xi по условию i = 1 значение x1
записывается в ОЗУ для дальнейшего использовании в алгоритме и в буферную память БП1 для дальнейшей
фильтрации и записи в БП2.
Далее, при поступлении измерения x2 производится его
сравнение с x1. В случае если x2 > x1 , то xi = 1 , наоборот - 0. Значение
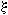 i
запоминается, для использования в последующем, при этом запоминается последнее
i
запоминается, для использования в последующем, при этом запоминается последнее
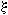 i
для сравнения с очередным
i
для сравнения с очередным
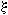 i+1 . В случае i = 2
i+1 . В случае i = 2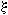 i ,
i ,
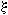 i
с
i
с 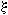 i+1 не сравнивается, поскольку
i+1 не сравнивается, поскольку
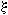 i от предыдущего измерения
просто нет, поэтому происходит переход к следующему блоку - определения разности между очередным
измерением xi и предыдущим xi-1 , то есть решается формула
i от предыдущего измерения
просто нет, поэтому происходит переход к следующему блоку - определения разности между очередным
измерением xi и предыдущим xi-1 , то есть решается формула
 x = | xi-xi-1|.
Далее сравнивается
x = | xi-xi-1|.
Далее сравнивается
 x с заданным удвоенным значение погрешности дискретизации
x с заданным удвоенным значение погрешности дискретизации
 x
x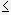 |2
|2 |. Если это условие выполняется,
измерение считается нормальным и поступает на запись в ОЗУ в качестве xi и в БП1. Если
|. Если это условие выполняется,
измерение считается нормальным и поступает на запись в ОЗУ в качестве xi и в БП1. Если
 x>|2
x>|2 |, то измерение аномальное. При этом производится
следующее. Во-первых, записывается в счётчик (
|, то измерение аномальное. При этом производится
следующее. Во-первых, записывается в счётчик ( i=m) факт аномального измерения и
сравнивается с числом М. В случае если m<М , то вычисляется и запоминается для дальнейшего
использования в алгоритме m´4
i=m) факт аномального измерения и
сравнивается с числом М. В случае если m<М , то вычисляется и запоминается для дальнейшего
использования в алгоритме m´4 . После этих манипуляций производится
дальнейшая обработка измерения.
. После этих манипуляций производится
дальнейшая обработка измерения.
Если xi+1>xi то исправленное значение xi+1
получается прибавлением к xi величины 2 , если наоборот, то 2
, если наоборот, то 2 из xj
вычитается. Поскольку неизвестно, кончилась ли последовательность пачки аномальных измерений {xj},(Причем
j может быть равно и “1”) , то прибавленные xi+1 на выход фильтра не подаются, а используются в самом
фильтре в качестве отсчета для сравнения с очередным измерением. То есть подаётся в блок решающий
задачу:
из xj
вычитается. Поскольку неизвестно, кончилась ли последовательность пачки аномальных измерений {xj},(Причем
j может быть равно и “1”) , то прибавленные xi+1 на выход фильтра не подаются, а используются в самом
фильтре в качестве отсчета для сравнения с очередным измерением. То есть подаётся в блок решающий
задачу: 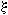 i=xi>xi-1 и
i=xi>xi-1 и
 x=|xi-xi-1|. Это
продолжается до тех пор, пока не кончится пакет аномальных измерений, или не выполнится условие m>M, то
есть не выработается сигнал “Сбой”, по которому процесс ввода информации должен прекратится до
выяснения причин сбоя.
x=|xi-xi-1|. Это
продолжается до тех пор, пока не кончится пакет аномальных измерений, или не выполнится условие m>M, то
есть не выработается сигнал “Сбой”, по которому процесс ввода информации должен прекратится до
выяснения причин сбоя.
Факт окончания последовательности аномальных измерений
определяется по изменению знака разности очередных измерений, то есть если
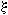 i
не равно
i
не равно 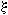 i-1. В этом случае производится переход к другой ветви программы. Во-первых,
снова производится определение модуля разности и сравнения его с величиной 4m
i-1. В этом случае производится переход к другой ветви программы. Во-первых,
снова производится определение модуля разности и сравнения его с величиной 4m . Эта
величина определяется как увеличившаяся зона неопределённости от последнего нормального измерения,
то есть 2
. Эта
величина определяется как увеличившаяся зона неопределённости от последнего нормального измерения,
то есть 2
 m
m 2 , где m число аномальных измерений в
пакете. Удвоение производится ввиду того, что зона неопределённости симметрична относительно
последнего нормального измерения.
2 , где m число аномальных измерений в
пакете. Удвоение производится ввиду того, что зона неопределённости симметрична относительно
последнего нормального измерения.
В том случае, если
 x
x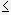 4m
4m ,
это измерение считается нормальным и алгоритм переходит к интерполяции зоны пакета аномальных
измерений, то есть получается xj - xi+j=(xi-xi+m+1)/(m+1). Расчет производится до тех пор,
пока j не станет больше m+1, то есть не дойдёт до последнего измерения. После этого интерполяция
заканчивается и значение m обнуляется. Одновременно с интерполяцией полученные значения измерений
поступают на запись в ОЗУ в качестве xi и в БП1.
,
это измерение считается нормальным и алгоритм переходит к интерполяции зоны пакета аномальных
измерений, то есть получается xj - xi+j=(xi-xi+m+1)/(m+1). Расчет производится до тех пор,
пока j не станет больше m+1, то есть не дойдёт до последнего измерения. После этого интерполяция
заканчивается и значение m обнуляется. Одновременно с интерполяцией полученные значения измерений
поступают на запись в ОЗУ в качестве xi и в БП1.
В том случае, если
 x>4m
x>4m то
производится исправление полученного значения xi путем вычисления xi*=xi+m+4m
то
производится исправление полученного значения xi путем вычисления xi*=xi+m+4m если
если
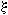 i=1 и xi*=xi+m-4m
i=1 и xi*=xi+m-4m если xi=0.
Далее интерполяция производится таким же образом. Однако вероятность такого события крайне мала.
если xi=0.
Далее интерполяция производится таким же образом. Однако вероятность такого события крайне мала.
После формирования массива информации в БП1 определяемого числом
информационных слов
 i=N информация поступает на фильтрацию по формуле (xi-1+2xi+xi+1)/4.
Такая фильтрация обеспечивает несмещённость по времени измерений и хорошее качество фильтрации.
Отфильтрованная информация поступает в буферную память БП2. Описанный алгоритм может быть изменён
добавлением, например, функции прореживания, нормирования массивов в БП2 по определённому закону и т.д.
Но это уже вопросы выходящие за рамки настоящей работы.
i=N информация поступает на фильтрацию по формуле (xi-1+2xi+xi+1)/4.
Такая фильтрация обеспечивает несмещённость по времени измерений и хорошее качество фильтрации.
Отфильтрованная информация поступает в буферную память БП2. Описанный алгоритм может быть изменён
добавлением, например, функции прореживания, нормирования массивов в БП2 по определённому закону и т.д.
Но это уже вопросы выходящие за рамки настоящей работы.
6. Итак, вопрос фильтрации при помощи вычислительных средств
рассмотрен. Необходимо отметить следующее. Борьба с помехами имеет комплексный характер. Она должна
производиться на всех этапах получения, передачи, обработки и регистрации измерительной информации.
Методически её можно определит в виде следующих направлений:
-
внедрение первичных преобразователей устойчивых к помехам и, особенно к аномальным измерениям;
- правильное размещение датчиков, качественный расчёт демпфирующих площадок;
- экранизация датчиков и аналоговая фильтрация в датчиках; - применение помехоустойчивых дискретных
элементов в цифровых частях канала передачи информации;
-
внедрение помехоустойчивых линий связи, в частности с частотной модуляцией, а также волоконно-оптических,
лазерных и т.п. линий связи;
- применение помехоустойчивого
кодирования, например на основе кодов Хемминга;
- правильный
выбор частотных диапазонов датчиков в соответствии со спецификой решаемых задач;
- проведение цифровой фильтрации по каждому из измеряемых параметров;
- проведение фильтрации по совокупности параметров (особенно взаимно коррелированных), на основе,
например, дискретных фильтров Калмана-Бьюси.
Каждое из этих направлений имеет свои преимущества и недостатки,
а также требует определённых затрат. Наибольший эффект может быть достигнут оптимальным выбором
совокупности вышеперечисленных методов.
ГЛАВА 6. НЕКОТОРЫЕ ВОПРОСЫ ВТОРИЧНОЙ ОБРАБОТКИ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
ИИС, по существу, предназначены для определения конечных
характеристик объекта. Измеряемый параметр сам по себе мало что даёт. Поэтому процесс измерений
состоит из нескольких этапов. Обычно их подразделяют на три этапа:
- первичная
обработка;
- вторичная обработка;
- анализ полученной
информации.
Первичная обработка обычно предусматривает приведения
измерительной информации по данному параметру к физическому виду. При этом учитываются методические
погрешности измерения, нелинейность датчиков и масштабирование. Например, при определении скорости
летательного аппарата необходимо учесть погрешности вносимые приёмником воздушного давления (ПВД),
нелинейность самого датчика и привести его к единице измерения. Кроме того, производится фильтрация
параметра и удаление аномальных измерений.
Под вторично обработкой обычно подразумевают определение
характеристики по совокупности измеренных параметров. Например, скороподъёмность летательного
аппарата определяется по ряду параметров, таких как высота, скорость, перегрузки, температура, давление
и влажность атмосферы и т.д.
Анализ совокупности характеристик производится с целью принятия
решений по объекту в целом и в настоящей работе рассматриваться не будет.
Исторически ИИС развивались следующим образом:
- ИИС на базе различных, в том числе оптических самописцев. При этом обработка информации производилась
в значительной мере вручную;
- Появление регистраторов на магнитной ленте и
стационарных ЭВМ позволило существенно автоматизировать процесс, но весь процесс обработки
информации осуществлялся уже после проведения измерений в стационарных условиях.
- Появление микропроцессорной техники предопределило тенденцию по переносу прежде всего первичной, а
затем и вторичной обработки на объект и выполнение обработки в реальном времени проведения измерений.
Кроме того, это позволило продвинуться и в области систем автоматического управления.
Однако, размещение средств обработки на объекте всегда
сталкивается с проблемой весогабаритных ограничений, особенно в областях авиации, космических
исследований и ряде других. Поэтому важно организовать процесс обработки информации таким образом, что
бы эта обработка требовала минимум ресурсов микропроцессорных вычислительных узлов, прежде всего
объёма запоминающих устройств (ОЗУ и ПЗУ), и расчеты выполнялись настолько быстро, чтобы процесс
обработки информации выполнялся в реальном масштабе времени. Этому в значительной мере способствует
оптимизация построения архитектуры системы, о чем разговор будет в соответствующей главе. Здесь будет
рассмотрены некоторые вопросы оптимизации процесса вычислений и объёмов требуемой памяти.
Кроме обычных логических операций и элементарных математических
преобразований процесс обработки измерительной информации требует использования различных
специальных и трансцендентных функций. К специальным функциям относятся разного рода тарировочные
функции и градуировочные поправки, а также некоторые другие зависимости. Рассмотрим некоторые из них:
1. Линеаризация производится в том случае, если физический
принцип измерения данного параметра обуславливает отличие статической характеристики (СХ) первичного
измерительного преобразователя (ПИП) от линейной.
В этом случае операция линеаризации заключается в суммировании к
реальной СХ поправки
 y1, где
y1, где
 y1 есть функция от x ( Рис.38).
y1 есть функция от x ( Рис.38).
 y1 = f(x) есть функция постоянная для данного ПИП. Поэтому для линеаризации данного ПИП
необходимо запоминание в памяти вычислительного устройства (ВУ) этой функции.
y1 = f(x) есть функция постоянная для данного ПИП. Поэтому для линеаризации данного ПИП
необходимо запоминание в памяти вычислительного устройства (ВУ) этой функции.
|
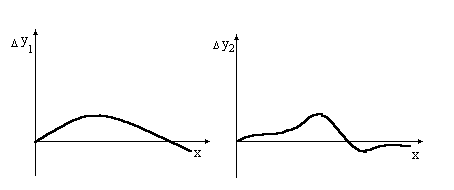
|
|
Рис.38
Рис.39 |
Введение градуировочных поправок вызвано тем, что
конструктивная реализация ПИП обуславливает появление инструментальных погрешностей, которая
выражается как неизменная для данного ПИП и может быть выражена в виде функции
 y2 = f(x)
(Рис.39). При этом
y2 = f(x)
(Рис.39). При этом
 y1 и
y1 и
 y2 могут быть объединены суммированием.
Таким образом, при первичной обработке производится суммирование градуировочных поправок
y2 могут быть объединены суммированием.
Таким образом, при первичной обработке производится суммирование градуировочных поправок
 y
представляющей собой функцию
y
представляющей собой функцию
 y = f(x), которая должна хранится в памяти ИИС.
y = f(x), которая должна хранится в памяти ИИС.
Умножением результатов измерений на коэффициент
масштабирования приводят результат измерения к физическому виду, то есть выраженным в обусловленных
единицах измерения. Эти операции совместно с фильтрацией, удалением аномальных измерений,
интерполяцией и составляют первичную обработку измерительной информации.
Вторичная обработка заключается в выполнении математических
преобразований вида:
X = f(p1 . . . pn; M1 . . . Mm), где Х - исследуемая
характеристика объекта; рi - измеряемые параметры; Мm - коэффициенты.
Характер коэффициентов может быть двоякий - постоянные
коэффициенты и коэффициенты, являющиеся функцией одного, или нескольких параметров. Например,
физические константы входят в решение как постоянные коэффициенты и функциями не являются. Другие
коэффициенты, например параметры стандартной атмосферы, погрешности метода и пр. выражаются как
функции. Например, функция Vв = f(M), где Vв - воздушная скорость, M - число Маха (Рис.40)
|
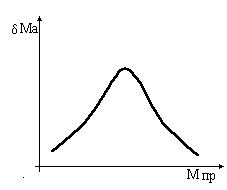
|
|
Рис.40 |
Общее число СФ для решения той, или иной задачи колеблется в
разных пределах. Однако, ориентировочно можно принять, что их число сравнимо с числом параметров и, как
правило, больше. Точную цифру мы, конечно, дать не можем, да и в этом нет необходимости, поскольку и так
ясно, что задача хранения СФ является достаточно важной, чтобы её здесь рассмотреть.
2. Математическая обработка результатов измерений заключает в
себя ряд логических, арифметических, трансцендентных операций и пр. преобразований. При этом наиболее
трудоёмкими являются трансцендентные операции ( sin, cos, tg , ctg , ln , lg , ex и пр.). В вычислительной математике в
применении к ЭВМ рекомендуется представление таких функций в виде рядов, то есть сведение к
арифметическим операциям. Однако это требует большого машинного времени и затрудняет обработку
информации в реальном масштабе времени. В связи с этим более предпочтительным является хранение таких
функций в виде таблиц. Однако при этом требуются большие объемы памяти.
Таким образом, СФ включают в себя градуировочные характеристики
ПИП, коэффициенты и поправки функционально зависящие от параметров и трансцендентные функции. Они
могут быть реализованы или таблично, что требует больших объёмов памяти, но быстро вычисляются, или в
виде коэффициентов степенных рядов, что требует значительно меньше объёмов памяти, но требует большого
времени для вычислений. Кроме того, разложение в ряды случайных функций крайне затруднительно.
Проблема состоит в том, какой найти способ реализации СФ, который требовал бы минимума объёмов памяти и
затрат времени на вычисления.
Если рассматривать СФ как некие случайные функции, то можно
поставить вопрос об их дискретизации, или квантованию по аргументу. При этом, применяя кусочно-линейную
интерполяцию, можно использовать математический аппарат рассмотренный выше, а именно формулы:
______
 x = 3
x = 3
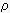 min
min
 и
и
 x =
50tg
x =
50tg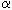 max /2
max /2 . Здесь диапазон функции y принимается за единицу,
. Здесь диапазон функции y принимается за единицу,
 в % от этого диапазона;
в % от этого диапазона;
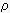 min - минимальный радиус кривизны;
min - минимальный радиус кривизны;
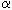 max -
максимальный угол наклона функции.
max -
максимальный угол наклона функции.
Выбор формул производится по следующему критерию: если
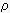 min³1 то выбирается первая формула, а если
min³1 то выбирается первая формула, а если
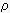 min<1 -
то вторая. При помощи этих формул определяется интервал
min<1 -
то вторая. При помощи этих формул определяется интервал
 x . Разделив диапазон изменений (х)
на этот интервал получим число интервалов а, следовательно, и число значений (аi) СФ находящихся в
памяти. Определение текущего значения функции производится по формуле: y = ai + bix , где ai
- ближайшее значение табличных значений функции к текущему её значению от начала координат, bi = (аi+1
- ai)/
x . Разделив диапазон изменений (х)
на этот интервал получим число интервалов а, следовательно, и число значений (аi) СФ находящихся в
памяти. Определение текущего значения функции производится по формуле: y = ai + bix , где ai
- ближайшее значение табличных значений функции к текущему её значению от начала координат, bi = (аi+1
- ai)/ x , где
x , где
 x шаг разбиения аргумента функции.
x шаг разбиения аргумента функции.
Всё это верно в том случае, если интервал
 x
равномерен. Как правило
x
равномерен. Как правило
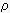 min на разных интервалах различно, поэтому такое
представление функции избыточно. Адаптивный подход, то есть изменение интервалов
min на разных интервалах различно, поэтому такое
представление функции избыточно. Адаптивный подход, то есть изменение интервалов
 x в
зависимости от кривизны позволяет уменьшить число интервалов, но при этом усложняется алгоритм
вычисления и увеличивается требуемый объем памяти, поскольку нужно вводить в таблицу не только
значения функции на дискретах, но и значения интервалов между ними, а, в конечном счёте, никакого
выигрыша мы не получаем, поэтому применение адаптивных подходов в этом вопросе вряд ли можно признать
целесообразным. Как известно из тригонометрии и алгебры все трансцендентные функции можно привести
к парным преобразованиям: cos x - arccos x и ex - ln x.
x в
зависимости от кривизны позволяет уменьшить число интервалов, но при этом усложняется алгоритм
вычисления и увеличивается требуемый объем памяти, поскольку нужно вводить в таблицу не только
значения функции на дискретах, но и значения интервалов между ними, а, в конечном счёте, никакого
выигрыша мы не получаем, поэтому применение адаптивных подходов в этом вопросе вряд ли можно признать
целесообразным. Как известно из тригонометрии и алгебры все трансцендентные функции можно привести
к парным преобразованиям: cos x - arccos x и ex - ln x.
Здесь можно принять два решения: или табулировать все четыре, или
только два исходных и использовать эти таблицы и для обратных преобразований методом, основанным на
рекуррентной итерации.
|
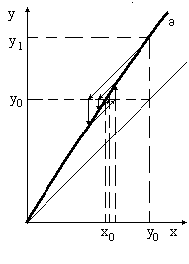
|
|
Рис.41 |
Положим, что f(x) представляет собой некоторую кривую (а) (Рис.41). При
этом нам известна y(x) , необходимо определить x . Подадим y0 на вход x, мы получим y1. Величина
y0-y1= 1y. Будем считать, что
1y. Будем считать, что
 1y линейно связана с
1y линейно связана с
 1x, тогда определим y2=y1(x1+
1x, тогда определим y2=y1(x1+ 1y). Далее определим
1y). Далее определим
 2y=y0-y2 и определим y3(x)=f(y2+
2y=y0-y2 и определим y3(x)=f(y2+ y2) и так далее.
y2) и так далее.
Общий
член рекуррентного ряда: fn(xn)=f[xn-1+ fn-2(xn-1)]. Рекуррентный ряд
при n
fn-2(xn-1)]. Рекуррентный ряд
при n
 сходится. При
сходится. При
 fn(xn) меньшем, чем заданная допустимая
погрешность процесс поиска прекращается и (х) считается найденным. Практическая апробация этого метода
показывает, что достаточно нескольких шагов чтобы найти искомое значение функции.
fn(xn) меньшем, чем заданная допустимая
погрешность процесс поиска прекращается и (х) считается найденным. Практическая апробация этого метода
показывает, что достаточно нескольких шагов чтобы найти искомое значение функции.
Можно поиск организовать по другому. А именно: область поиска
разделить пополам и задать любое х. Если область по первому знаку совпадает с заданной функцией, то в
искомом числе ставится в первом разряде 1. Если нет, то нуль. Далее разбивается половина, в которой
находится функция ещё надвое и операция повторяется. Процесс продолжается до заполнения всего кода
адреса. Это можно назвать диатомическим процессом. Преимущество метода в более чёткой определённости в
затрачиваемом времени. Но предыдущий метод в среднем более экономен в 2-3 раза.
Необходимо отметить, что использование таблиц прямых функций для
получения обратных возможно только в том случае, если прямая функция однозначно определена, то есть
данному значению y соответствует одно значение x . Для ряда функций характерно может быть то, что
положение по оси x их максимальной кривизны не совпадает с положением экстремума. В этом случае расчет
числа интервалов может производиться по формуле:
_____
 x
=
x
=

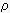 min(x)
min(x)
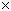 cos(arctg |x’max| M,
cos(arctg |x’max| M,
где М - коэффициент, учитывающий соотношение масштабов по x и y. Расчеты, проведенные на основе
фактического материала, показывают, что число интервалов для создания таблиц, исчисляется десятками,
иногда сотнями но, во всяком случае, объём информации значительно меньше, чем при составлении таблиц
функций без применения линейной интерполяции.
ГЛАВА 7. ВОПРОСЫ ТЕОРИИ ОБРАТНОЙ СВЯЗИ В ПРИЛОЖЕНИИ К ИИС
Измерения производятся, естественно, для того, чтобы на их основе
принимать какие-то решения. Если эти решения производит человек и воздействует как оператор на объект,
мы имеем систему с ручным управлением. Если решения принимает какое то техническое устройство - мы
имеем автоматическую систему управления. И в том и в другом случае, если измеряются параметры того
объекта, который на основе этих измерений управляется - мы имеем систему с обратной связью.
|
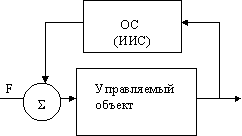
|
|
Рис.42 |
Эффективность управления зависит от всех элементов системы, в
том числе и измерительной системы. Но особое значение в этом случае имеет обратная связь. В общем случае
в приложении к сложным объектам структура обратной связи (ОС) имеет вид показанный на Рис.42. На объект
оказывает влияние совокупность некоторых внешних воздействий F. Информация о результатах этого
воздействия через обратную связь (ИИС) поступает на решающее устройство ( ), где
складывается с продолжающимся воздействием, обрабатывается и снова поступает на вход управляемого
объекта. Решающим устройством может быть как человек (оператор), так и некоторое автоматическое
устройство, а иногда и совместно. Количество параметров контролируемых с помощью ИИС и количество
воздействий прикладываемых к объекту не определено. Сложность такой структуры такова, что решение
проблемы оптимизации системы управления представляет собой исключительную сложность. Имеется масса
различных теоретических наработок и практических подходов. Тем не менее, поиск новых теоретических
концепций ещё далеко не завершён и если мы попытаемся предложить ещё какие то идеи, хуже от этого не
будет. В настоящей работе предлагается уточнить некоторые вопросы обратной связи. Исследования
проводятся на упрощенной модели одноканального усилителя с ОС, результаты которых мы попытаемся
распространить и на более общие случаи.
), где
складывается с продолжающимся воздействием, обрабатывается и снова поступает на вход управляемого
объекта. Решающим устройством может быть как человек (оператор), так и некоторое автоматическое
устройство, а иногда и совместно. Количество параметров контролируемых с помощью ИИС и количество
воздействий прикладываемых к объекту не определено. Сложность такой структуры такова, что решение
проблемы оптимизации системы управления представляет собой исключительную сложность. Имеется масса
различных теоретических наработок и практических подходов. Тем не менее, поиск новых теоретических
концепций ещё далеко не завершён и если мы попытаемся предложить ещё какие то идеи, хуже от этого не
будет. В настоящей работе предлагается уточнить некоторые вопросы обратной связи. Исследования
проводятся на упрощенной модели одноканального усилителя с ОС, результаты которых мы попытаемся
распространить и на более общие случаи.
1. Понятие “обратная связь” применительно к электрическим и
электронным схемам, казалось бы, не должно вызывать неясностей, спустя большой период времени после
выхода в свет монографии Г.Боде и большого количества научной и учебной литературы. Однако дискуссия
вокруг связанных с обратной связью вопросов продолжается. Например, “ ...уместно подчеркнуть
субъективность термина “обратная связь””[14]. Нет единства в определении понятия ОС и ее сущности в
целом, наличия и вида ОС (положительная или отрицательная, по току или по напряжению, параллельная или
последовательная)[15]. “Ошибки в описании свойств усилительных цепей с обратной связью, в основном,
вызваны формальным использованием математического аппарата и они получили столь широкое
распространение, что нет необходимости ссылаться на конкретные литературные источники. Эти ошибки
могли оставаться незамеченными только потому, что до последнего времени радиотехнические устройства
отрабатывались, как правило, экспериментально, а их математический расчет выполнялся приближённо и
играл вспомогательную роль. Однако внедрение микроэлектроники и, как следствие, развитие методов
математического моделирования и машинного проектирования радиотехнических цепей, настолько требует
уточнения многих существующих представлений об усилителях с обратной связью и устранения ошибок в
технической и, в особенности, учебной литературе”[16].
Особенно бросается в глаза тот факт, что подход к анализу систем
различного типа (линейных, нелинейных, импульсных, цифровых и т.п.) весьма различен. Отличаются способы
применения классических методов анализа и в зависимости от того, рассматривается радиотехническая
система или устройство автоматического регулирования.
В настоящей работе делается попытка разработки такого метода
анализа устройств с ОС, который не имел бы ограничений, накладываемы на систему с ОС в монографии Боде,
то есть метода не использующего дифференциальных уравнений. Таким методом можно было бы анализировать
более широкий класс систем, он обладал бы большей универсальностью. Действительно, линейным
дифференциальным уравнением может описываться только линейная система, которая является идеализацией
реального устройства. Поэтому применение метода анализа, основанного на линейных дифференциальных
уравнениях, к реальным устройствам может привести к ошибкам, а для существенно нелинейных устройств с
ОС применение его вообще невозможно[17].
2. Среди понятий теории обратной связи больше всего расхождение в
работах различных авторов связано с понятием “знак обратной связи”. Это понятие чаще всего
определяется следующим образом: “Обратная связь может быть положительной или отрицательной в
зависимости от того, суммируется выходная переменная с её входной величиной или вычитается из неё.”[17 ].
Подобное определение приводится и во многих других работах.
Встречается также следующее определение: “...усилители с
обратной связью обладают положительной обратной связью, когда внешнее усиление возрастает при
одновремённом возрастании влияния параметров лампы, либо обладает отрицательной обратной связью,
когда усиление падает при одновремённом соответственном уменьшении влияния изменений в лампе.”[18].
Существуют и другие определения, а иногда определения знака обратной связи вообще не приводится.
Применение первого из вышеприведенных определений неудобно,
поскольку в практике разработки аппаратуры обычно подразумевается, что знак обратной связи является
структурным признаком конкретного устройства и не зависит от вида и характеристик входного сигнала. То
же подразумевается и во втором определении. Согласно первому определению, знак ОС зависит от вида и
характеристик сигнала. Действительно, если подать на вход устройства с ОС сигнал в виде
синусоидального напряжения, то за счет реактивности цепи ОС выходной сигнал будет иметь фазовый сдвиг
относительно входного. Этот фазовый сдвиг при изменении частоты входного сигнала меняется и при
замыкании контура ОС выходная переменная может при одних значениях частоты складываться с входной, при
других - вычитается. Поскольку на входе всегда есть детерминированный или случайный сигнал (строго
говоря, с бесконечной шириной полосы частот) и фазочастотная характеристика устройства с ОС всегда
нелинейна, то любое реальное устройство с ОС, согласно первому определению, является одновремённо
устройством как с положительной, так и отрицательной связью.
Было бы желательно иметь такое определение знака ОС, которое
отражало бы структуру устройства и не зависело от вида и характеристик входной переменной.
Второе определение, хотя и не достаточно чётко, связывает знак ОС
со структурой усилителя с ОС, однако его недостаток состоит в том, что определением представлено
следствие, влияние знака ОС, а не его сущность. Как правило, в приложениях понятия ОС подразумевается,
что знак ОС является признаком структуры устройства и зависит, например, от числа активных элементов и
полярности подключения трансформаторов.
Поскольку понятие знака ОС является одним из основных в теории
обратной связи, то прежде чем перейти к изложению основного материала необходимо остановиться на
определении этого понятия. С целью установления однозначной связи знака ОС со структурой устройства
использовано понятие “инверсия”.
ОПРЕДЕЛЕНИЕ: Инверсия - такое действие над
функцией f(t), при котором все составляющие её спектра изменяют фазу на p. Инверсия
происходит в таких устройствах, как, например, транзисторный каскад с общим эмиттером, трансформатор
при определённом подключении обмоток и т.д. Однако в чистом виде получить инверсию невозможно, так как
она всегда сопровождается искажением спектра сигнала за счет того, что реальные элементы устройств
всегда обладают реактивными составляющими своих характеристик как многополюсников.
|
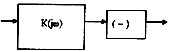
|
|
Рис.43 |
Поэтому, например, транзисторный усилительный каскад с общим
эмиттером должен быть изображён в виде структурной схемы (Рис.43), где знаком - ( - ) обозначен инвертор, а [K(jw)] обозначает способность каскада усиливать сигнал и изменять его частотный спектр. Наличие
инверсии характеризует структуру устройства и не зависит от характеристик входного сигнала.
Устройство, в котором производится инвертирование, обычно
называется инвертором. Если сигнал последовательно проходит нечетное число инверторов, то на выходе он
получается инвертированным, если четное - не инвертированным.
ОПРЕДЕЛЕНИЕ: Обратная связь положительна, если сигнал,
пройдя по замкнутому контуру обратной связи, не инвертируется и отрицательна, если сигнал
инвертируется.
В коэффициенте передачи цепи наличие инверсии обозначается
знаком минус.
Данное определение позволяет более строго обосновать
существующее разделение всех устройств с обратными связями на два класса - устройства с положительной
ОС, применяемых для осуществления автогенерации, в качества регенеративных усилителей, корректирующих
цепей и т.п., и устройства с отрицательной ОС, широко применяемые как в радиотехнике для стабилизации
параметров схем и получения широкой полосы пропускания, так и в устройствах автоматического
регулирования и управления.
3. В качестве объекта анализа взят электронный усилитель, в
котором имеется пассивная часть, которая определяет частотные и временные характеристики усилителя, и
активные элементы, которые, после учета их реактивностей в пассивной части, могут рассматриваться как
безинерционные, инвертирующие, с коэффициентом усиления А. В отношении нелинейности и задержек при
необходимости будут делаться оговорки. Цепи усилителя ограничиваются неминимальнофазовыми,
лестничного типа.
В качестве входного воздействия принимается напряжение, при
необходимости выражаемое в комплексной форме[ 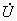 ], в виде функции времени [u(t)]
или частоты [U(
], в виде функции времени [u(t)]
или частоты [U( )] [19]. На Рис.44 изображена структурная схема прямой цепи. Пассивная часть её
характеризуется передаточной функцией
)] [19]. На Рис.44 изображена структурная схема прямой цепи. Пассивная часть её
характеризуется передаточной функцией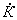 . Для пассивной цепи |
. Для пассивной цепи |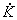 |
| 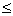 1 .
1 .
|

|
|
Рис.44 |
Передаточная функция цепи, изображённой на Рис.44 равна 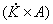 при отсутствии инверсии и
при отсутствии инверсии и 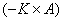 при её наличии.
Рассматриваемая цепь не взаимна, так как она включает в себя активный элемент. Принято, что от выхода ко
входу сигнал не передаётся.
при её наличии.
Рассматриваемая цепь не взаимна, так как она включает в себя активный элемент. Принято, что от выхода ко
входу сигнал не передаётся.
Описанная цепь охватывается цепью обратной связи с передаточной
функцией 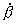 , которая принимается невзаимной [20], передающей сигнал только в одном
направлении – с выхода на вход прямой цепи (Рис.45). Известно [19,11,21],что передаточная функция усилителя с
ОС выводится из передаточных функций прямой и обратных цепей путем решения системы уравнений и
определяется выражением:
, которая принимается невзаимной [20], передающей сигнал только в одном
направлении – с выхода на вход прямой цепи (Рис.45). Известно [19,11,21],что передаточная функция усилителя с
ОС выводится из передаточных функций прямой и обратных цепей путем решения системы уравнений и
определяется выражением:
|
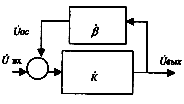
|
|
Рис.45 |
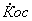 =
= 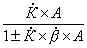 (7.1)
(7.1)
Недостаток такого способа вывода выражения передаточной функции
усилителя с ОС заключается в том, что он не отражает сущности процесса происходящего в усилителе, что, в
свою очередь, затрудняет анализ полученного выражения, в том числе определение устойчивости усилителя
с ОС. Ставится задача разработать такой способ вывода выражения передаточной функции усилителя с
обратной связью, который был бы лишён этих недостатков, и обосновать его применение для основных видов
устройств с ОС. В математическом плане ставится задача разработать такой метод анализа устройств с ОС,
который бы не требовал применения теории линейных дифференциальных уравнений, так как она имеет тот
недостаток, что, строго говоря, не может быть применена для анализа нелинейных систем, к которым
относится любое реальное устройство с ОС, хотя в отдельных случаях её применение и оправдано.
4. Рассматривая структурную схему (Рис.45) усилителя с ОС можно сделать
вывод, что сигнал, поданный на вход схемы, обходит замкнутый контур и снова подаётся на вход, откуда
вторично обходит замкнутый контур и снова подаётся на вход, и так бесконечное число раз.
На входе усилителя с ОС происходит сложение сигналов поданного
на вход в виде напряжения 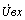 , с этим же сигналом, совершившим один обход контура
ОС, два, три и так далее, до бесконечного числа раз.
, с этим же сигналом, совершившим один обход контура
ОС, два, три и так далее, до бесконечного числа раз.
Передаточная функция прямой цепи усилителя с ОС равна (Рис.45):
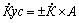 .
.
Передаточная функция, составленная из прямой цепи и цепи ОС,
равна:
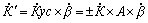 .
(7.2)
.
(7.2)
Если сигнал 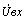 обходит контур
дважды, то это равносильно прохождению сигнала через четырёхполюсник с передаточной функцией -
обходит контур
дважды, то это равносильно прохождению сигнала через четырёхполюсник с передаточной функцией - 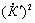 , если n раз, то с передаточной функцией -
, если n раз, то с передаточной функцией - 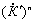 .
.
Таким образом, напряжение на выходе усилителя с ОС равно:
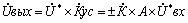 .
.
Но 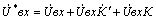
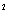
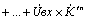 при
при 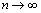 .
.
Или: 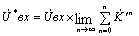 .
.
Следовательно: 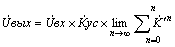 .
.
Или: 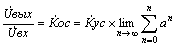 .
(7.3)
.
(7.3)
Известно [22], что предел ряда 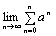 , при
, при 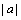 < 1, равен
< 1, равен 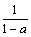 .
.
Отсюда, при 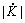 <1,
<1, 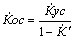 ,
или [19,11,23,24]:
,
или [19,11,23,24]: 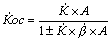 . (7.4)
. (7.4)
Получена такая же формула (7.4), как и формула полученная путём
решения системы уравнений (7.1). Пользуясь представлением формулы (7.4) в виде степенного ряда (7.3) можно
составить два варианта эквивалентных схем усилителей с ОС (Рис.46,47).
|
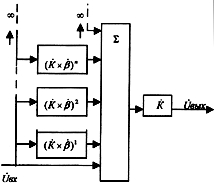
|
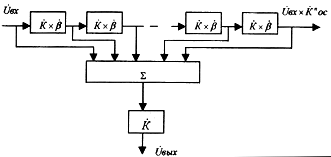
|
|
Рис.46 |
Рис.47 |
Знак в знаменателе (7.4) зависит от того, положительной или
отрицательной связью охвачен усилитель. Известно [19] что передаточная функция цепи, в частности контура
обратной связи, может быть представлена в виде: 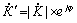 (7.5) , то есть вектора. Производя замену в
Рис.47 (7.3) согласно (7.5), коэффициент передачи усилителя можно представить в виде суммы векторов (Рис.48)
(7.5) , то есть вектора. Производя замену в
Рис.47 (7.3) согласно (7.5), коэффициент передачи усилителя можно представить в виде суммы векторов (Рис.48)
|
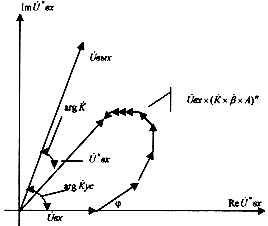
|
|
Рис.48 |
|
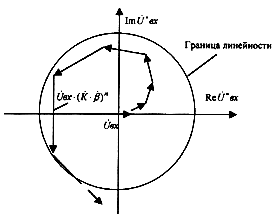
|
|
Рис.49 |
Из Рис.48 видно, что при |K|<1, независимо от фазового сдвига,
сумма векторов имеет предел 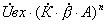 в виде вектора
в виде вектора 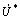 , из которого, при
прохождении сигнала через прямую цепь, формируется выходное напряжение
, из которого, при
прохождении сигнала через прямую цепь, формируется выходное напряжение 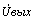 , откуда можно
сделать вывод, что здесь показан устойчивый режим. На Рис.49 показано, что при |K|>1, сумма векторов
предела не имеет, точнее, её предел определяется границами линейности цепи. Такой режим является
неустойчивым. Сложение производится на комплексной плоскости
, откуда можно
сделать вывод, что здесь показан устойчивый режим. На Рис.49 показано, что при |K|>1, сумма векторов
предела не имеет, точнее, её предел определяется границами линейности цепи. Такой режим является
неустойчивым. Сложение производится на комплексной плоскости 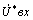 .
.
К такому выводу можно прийти и аналитически. Ряд (7.3) мажорируется
рядом 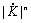 , который при
, который при 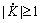 не имеет предела.
не имеет предела.
Поскольку сложение производится в комплексной форме, время
исключено, то есть взаимосвязь между векторами только причинная, но не временная. Сложение векторов
происходит мгновенно, поэтому при 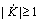 вектор суммы
вектор суммы 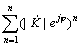 вращается со
скоростью равной бесконечности, то есть частота вектора
вращается со
скоростью равной бесконечности, то есть частота вектора 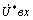 равна бесконечности. Естественно,
что такой сигнал не может пройти через реальную цепь, что позволяет сделать вывод об устойчивости
усилителя, если
равна бесконечности. Естественно,
что такой сигнал не может пройти через реальную цепь, что позволяет сделать вывод об устойчивости
усилителя, если 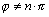 (при n = 0,1,2, …
(при n = 0,1,2, …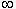 ). Такой вывод соответствует критерию
Найквиста. Однако если сигнал, проходя по цепи контура ОС, приобретает временную задержку
). Такой вывод соответствует критерию
Найквиста. Однако если сигнал, проходя по цепи контура ОС, приобретает временную задержку
 t,
то частота вращающегося вектора будет конечна и усилитель может стать неустойчивым, даже если годограф
вектора коэффициента передачи разомкнутой цепи ОС не охватывает точку с координатами (-1;0). Более
подробно вопрос о применимости критерия Найквиста будет рассмотрен ниже.
t,
то частота вращающегося вектора будет конечна и усилитель может стать неустойчивым, даже если годограф
вектора коэффициента передачи разомкнутой цепи ОС не охватывает точку с координатами (-1;0). Более
подробно вопрос о применимости критерия Найквиста будет рассмотрен ниже.
Устойчивость схемы (Рис.45) не зависит от того, обладает ли
полубесконечная линия, составленная из звеньев 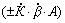 , конвективной или абсолютной
неустойчивостью[24,26].
, конвективной или абсолютной
неустойчивостью[24,26].
5. Рассмотрим теперь вопрос о влиянии передаточной функции на
знак обратной связи. Необходимость этого обуславливается тем, что выше было дано определение знака ОС с
использованием понятия инверсии и упоминалось, что оно позволяет считать знак ОС независимым от
частотных характеристик цепи. Причина этого объясняется ниже.
Любая передаточная функция действительной и положительной цепи может быть,
представлена в виде непрерывной дроби, то есть, действительную и положительную цепь можно представить
в виде схемы показанной на Рис.50 [19]:
|
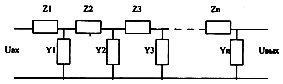
|
|
Рис.50 |
Каждая из пар (Zn;Yn) представляет собой элементарное звено, передаточную функцию которого можно
обозначить - 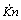 . Тогда передаточную функцию всей цепи можно представить в виде [19,27]:
. Тогда передаточную функцию всей цепи можно представить в виде [19,27]: 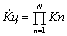 . Каждое из звеньев имеет в общем случае комплексный коэффициент передачи. В некоторый,
достаточно малый, начальный период времени переходного процесса, являющегося реакцией на единичный
скачёк поданный на вход цепи, выходное напряжение можно аппроксимировать выражением:
. Каждое из звеньев имеет в общем случае комплексный коэффициент передачи. В некоторый,
достаточно малый, начальный период времени переходного процесса, являющегося реакцией на единичный
скачёк поданный на вход цепи, выходное напряжение можно аппроксимировать выражением: 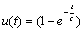 ;
где
;
где 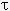 - постоянная времени цепи.
- постоянная времени цепи.
Эквивалентная схема элементарного звена (Zn;Yn) может быть
представлена в виде набора из трёх элементов - активного сопротивления (R), индуктивности (L) и ёмкости (С),
которые могут представлять собой как отдельные конструктивные элементы, так и электрические
характеристики конструкции элементов и монтажа.
Переходная функция звена может быть выражена формулой [19]:
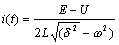 (
(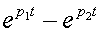 ),
),
где: 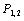 - пара сопряжённых корней, равных:
- пара сопряжённых корней, равных: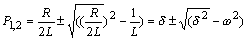 .
.
Переходные функции при разных соотношениях
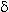 и
и
 показаны на Рис.51.
показаны на Рис.51.
|
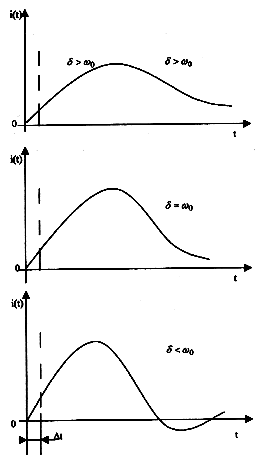
|
|
Рис.51 |
При небольшой величине
 t все звенья могут считаться
апериодическими, инерционными звеньями, так как начальный участок переходной функции может
аппроксимироваться функцией:
t все звенья могут считаться
апериодическими, инерционными звеньями, так как начальный участок переходной функции может
аппроксимироваться функцией: 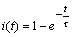 . Производная при t = 0 положительна для этой функции.
Известно [19], что при передаче на вход цепи, представляющее элементарное звено, напряжения u(t) = 1 при t<0
и u(t)=0 при t>0, переходная функция примет вид
. Производная при t = 0 положительна для этой функции.
Известно [19], что при передаче на вход цепи, представляющее элементарное звено, напряжения u(t) = 1 при t<0
и u(t)=0 при t>0, переходная функция примет вид 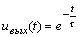 . Если звено имеет усиливающий активный
элемент, то
. Если звено имеет усиливающий активный
элемент, то 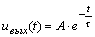 . При соединении таких звеньев в цепь, передаточная функция будет иметь вид:
. При соединении таких звеньев в цепь, передаточная функция будет иметь вид: 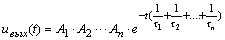 , или, если все звенья одинаковы:
, или, если все звенья одинаковы: 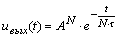 . Производная такой функции при t=0 имеет тот
же знак, что и производная единичного скачка, поданного на вход цепи, которая равна бесконечности при t=0.
. Производная такой функции при t=0 имеет тот
же знак, что и производная единичного скачка, поданного на вход цепи, которая равна бесконечности при t=0.
Если на вход усилителя подаётся напряжение 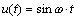 равное
0 при
равное
0 при 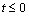 , то на выходе контура ОС будет отклик также равный нулю при
, то на выходе контура ОС будет отклик также равный нулю при 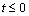 , и
производная его, при t=0, будет иметь тот же знак, что и производная входной функции. Это значит, что от t=0
до некоторого времени полярность отклика на входное воздействие будет совпадать с полярностью
входного воздействия, то есть знак ОС будет определяться только наличием, или отсутствием инверсии. Из
вышеизложенного следует, что соотношение характеристик входной функции и её отклика при t "
0 и при t " ¥ настолько отличаются, что выводы, полученные при анализе
установившегося режима, могут быть противоположны выводам, полученным при анализе переходного режима.
, и
производная его, при t=0, будет иметь тот же знак, что и производная входной функции. Это значит, что от t=0
до некоторого времени полярность отклика на входное воздействие будет совпадать с полярностью
входного воздействия, то есть знак ОС будет определяться только наличием, или отсутствием инверсии. Из
вышеизложенного следует, что соотношение характеристик входной функции и её отклика при t "
0 и при t " ¥ настолько отличаются, что выводы, полученные при анализе
установившегося режима, могут быть противоположны выводам, полученным при анализе переходного режима.
Действительно, если синусоидальная функция, подаваемая на вход
цепи при t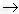
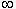 , имеет по сравнению с её откликом на выходе сдвиг по
фазе равный
, имеет по сравнению с её откликом на выходе сдвиг по
фазе равный
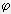 , то при t
, то при t 0 такой сдвиг стремится к нулю. То есть, можно
считать, что в области t
0 такой сдвиг стремится к нулю. То есть, можно
считать, что в области t 0 входное синусоидальное воздействие синфазно со своим
откликом на выходе, в то время как при t
0 входное синусоидальное воздействие синфазно со своим
откликом на выходе, в то время как при t
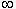 эти функции могут быть
противофазны.
эти функции могут быть
противофазны.
Анализ процессов, происходящих в усилителе с ОС, удобно
рассматривать на примере усилителя, в котором, при разомкнутой цепи контура ОС, реакцией на входное
воздействие в виде единичного скачка будет также скачёк, изменяющийся только по амплитуде и имеющий
задержку t. Выводы, полученные для такого усилителя, могут быть распространены и на
усилитель с ограниченной полосой пропускания, что будет показано ниже.
6. Как было показано выше, переходную функцию цепи контура
усилителя с ОС, как реакцию на единичный положительный скачёк, можно аппроксимировать, при достаточно
малом  t от t=0, функцией:
t от t=0, функцией: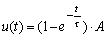 , или
, или 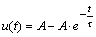 . Для сигнала, обходящего контур
n раз:
. Для сигнала, обходящего контур
n раз:
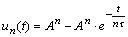 , откуда
, откуда 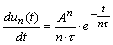 .
.
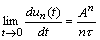 ;
; 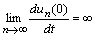 при. А > 1.
при. А > 1.
Следовательно, при коэффициенте усиления А > 1, независимо от
постоянной времени t, производная переходной функции стремится к бесконечности.
Амплитуда также стремится к бесконечности, Пределом такой переходной функции можно считать
ступенчатую функцию с амплитудой равной бесконечности. Из этого следует, что линейная диспергирующая
цепь, включённая в контур ОС, обеспечивает, с одной стороны, ограниченную полосу пропускания, с другой
стороны, приводит к процессу суммирования, аналогичном суммированию в импульсном усилителе, который
будет рассмотрен ниже.
7. Поскольку импульсные усилители в настоящее время получили
широкое распространение и для получения широкой полосы пропускания, при которой может достаточно
качественно передаваться форма импульса, широко применяется обратная связь, представляет интерес
рассмотреть работу такого усилителя. Кроме того, ООС применяется и для формирования более широкой
полосы пропускания в широкополосных усилителях. Как было показано выше, анализ диспергирующего
усилителя может быть сведён к анализу импульсного усилителя.
Для анализа процесса, в данном случае, предполагается, что
имеется усилитель, с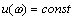 и с временной задержкой t, охваченный отрицательной ОС.
На вход усилителя подан единичный скачёк. На рис.52 показан процесс во времени, где
и с временной задержкой t, охваченный отрицательной ОС.
На вход усилителя подан единичный скачёк. На рис.52 показан процесс во времени, где 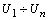 - это напряжения
- это напряжения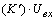 . Из графиков видно, что сумма напряжений
. Из графиков видно, что сумма напряжений 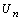 представляет собой колебательный процесс с амплитудой нарастающей по экспоненте при
представляет собой колебательный процесс с амплитудой нарастающей по экспоненте при 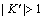 .
.
|
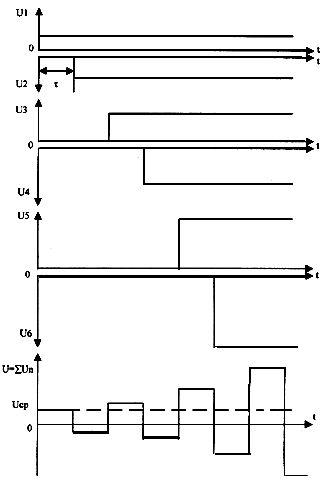
|
|
Рис.52 |
Период такого колебания равен: Т=2t. Частота несущей гармонической составляющей равна: . Следовательно, при уменьшении t до нуля,
. Следовательно, при уменьшении t до нуля, 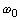 стремится к
бесконечности, то есть:
стремится к
бесконечности, то есть: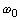 .
.
Поскольку процесс суммирования в усилителе с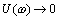 при w
при w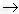 ¥ в конечном счёте, приводит к тем же результатам что и в усилителе с
¥ в конечном счёте, приводит к тем же результатам что и в усилителе с 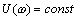 ,
вследствие того, что при n
,
вследствие того, что при n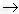
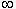 форма импульсов Un стремится к форме импульса с амплитудой
стремящейся к бесконечности. Однако в этом случае, при
форма импульсов Un стремится к форме импульса с амплитудой
стремящейся к бесконечности. Однако в этом случае, при 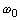
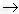
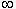 , сигнал
, сигнал 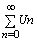 не сможет пройти через цепь с ограниченной полосой пропускания. Поэтому на выходе усилителя
напряжение будет равно средней величине суммы
не сможет пройти через цепь с ограниченной полосой пропускания. Поэтому на выходе усилителя
напряжение будет равно средней величине суммы 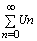 , определяемой с помощью формулы:
, определяемой с помощью формулы: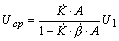 .
.
При этом усилитель будет устойчив. Однако при 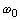 конечной
(если в цепи контура ОС имеются задержки) усилитель с ООС может генерировать колебания. Такой процесс
может быть в эмиттерном повторителе [28]. Вообще говоря, реальное устройство должно иметь конечную
частоту
конечной
(если в цепи контура ОС имеются задержки) усилитель с ООС может генерировать колебания. Такой процесс
может быть в эмиттерном повторителе [28]. Вообще говоря, реальное устройство должно иметь конечную
частоту 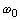 , хотя бы вследствие конечной скорости распространения входного возмущения и
конечных размеров устройства. Поэтому любое устройство может рассматриваться как устойчивое при
величине колебания с частотой
, хотя бы вследствие конечной скорости распространения входного возмущения и
конечных размеров устройства. Поэтому любое устройство может рассматриваться как устойчивое при
величине колебания с частотой 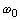 настолько малой, что ею можно пренебречь. Такой режим
работы усилителя с ООС можно назвать, например, квазиустойчивым. Вопрос об амплитуде колебаний в
настоящей работе не рассматривается, так как она определяется рядом факторов выходящих за её рамки.
настолько малой, что ею можно пренебречь. Такой режим
работы усилителя с ООС можно назвать, например, квазиустойчивым. Вопрос об амплитуде колебаний в
настоящей работе не рассматривается, так как она определяется рядом факторов выходящих за её рамки.
В любом случае, достаточным критерием устойчивости усилителя с
ООС является: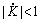 . В отношении импульсных усилителей такой критерий принят в работах [29,27,28,26].
. В отношении импульсных усилителей такой критерий принят в работах [29,27,28,26].
8. Теперь рассмотрим приложение метода степенного ряда к анализу
процессов в автогенераторе. Под автогенератором, в данном случае, подразумевается усилитель с
положительной ОС с модулем коэффициента передачи по контуру ОС большем единицы, с линейной
частотнозависимой пассивной частью цепи контура ОС. Считается, что в контуре ОС задержек, элементов с
неминимальнофазовыми АЧХ и отрицательных сопротивлений нет.
Сложение элементов ряда можно рассматривать как сложение
импульсов, с амплитудой стремящейся к бесконечности, что в случае с усилителем с ПОС приводит к
лавинообразному нарастанию напряжения в сторону возмущающего воздействия. Такое нарастание
происходит до тех пор, пока не наступит насыщение активного элемента.
При насыщении, подача на вход усилителя возмущающего воздействия
такого же знака, как и знак предыдущего возмущающего воздействия, не может вызвать реакцию на выходе
контура ОС. То есть, при насыщении обратная связь разрывается, наступает состояние устойчивости, из
которого усилитель может быть выведен возмущающим воздействием противоположного знака и достаточной
величины [29]. При этом снова происходит лавинообразный процесс, который переводит усилитель в другое
состояние насыщения. Для осуществления постоянных автоколебаний необходимо чтобы в усилителе с ОС
существовал источник знакопеременных возмущающих воздействий.
Источники знакопеременных возмущающих воздействий могут быть
реализованы различными способами, но одним из самых распространённых является колебательный контур,
свободные колебания которого есть синусоидальные колебания, имеющие положительные и отрицательные
полупериоды. При этом частота перебросов усилителя из одного устойчивого (насыщенного) состояния в
другое будет определяться частотой собственных колебаний контура. При таком представлении процесса
происходящего в автогенераторе, можно показать, что:
-при отсутствии в схеме усилителя источника знакопеременных
входных возмущающих воздействий, усилитель с ПОС является неустойчивым и стремится перейти в одно из
крайних состояний, насыщения или запирания. Если принять меры к тому, чтобы эти состояния были
достаточно устойчивы, то можно получить такое устройство, как триггер, если будет одно состояние
устойчивое, то можно получить одновибратор;
-обеспечение баланса фаз не является необходимым для работы
автогенератора, необходимо только чтобы соблюдались условия "раскачки" колебательного элемента
ОС.
9. В литературе по теории радиоцепей, теории автоматического
регулирования и технической кибернетике при рассмотрении теории устойчивости устройств с ОС, как
правило, приводится критерий устойчивости Найквиста [17,30,18,31,29 и др.]. Этот критерий, благодаря своей
математической наглядности и удобству в практическом применении, получил широкое распространение.
Однако, при этом не всегда достаточно строго учитываются те условия и ограничения, которые приводятся в
работах Найквиста и Боде [18,32].
Условия, накладываемые на систему с ОС, к которым применим
критерий Найквиста, следующие [18,32]:
-аналитичность коэффициента передачи 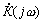 с
разорванной ОС;
с
разорванной ОС;
-линейность;
-отсутствие неминимальнофазовых цепей.
Кроме того, вывод об устойчивости или неустойчивости делается
тогда, когда переходные процессы прекращаются, то есть при t®¥ .
Если предположить, что 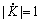 , то процесс в усилителе с ПОС при
подаче на вход синусоидального напряжения, может быть представлен, согласно формуле (7.3), в виде суммы
бесконечного количества синусоид, Причём, если сдвиг по фазе j между синусоидами равен
нулю или кратен 2p, то эта сумма будет представлять собой синусоиду с амплитудой равной
бесконечности, что соответствует режиму неустойчивости (Рис.53а):
, то процесс в усилителе с ПОС при
подаче на вход синусоидального напряжения, может быть представлен, согласно формуле (7.3), в виде суммы
бесконечного количества синусоид, Причём, если сдвиг по фазе j между синусоидами равен
нулю или кратен 2p, то эта сумма будет представлять собой синусоиду с амплитудой равной
бесконечности, что соответствует режиму неустойчивости (Рис.53а):
|
|
|
Рис.53 |
Если же сдвиг по фазе не равен нулю и не кратен 2p, то в данный момент времени количество
слагаемых синусоид 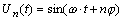 , при n=
, при n=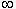 , как положительной, так и отрицательной
полярности, будет одинаково и равно бесконечности. Причём, величины напряжений
, как положительной, так и отрицательной
полярности, будет одинаково и равно бесконечности. Причём, величины напряжений 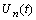 в этот
момент времени будут распределены по синусоидальному закону. Сумма же всех напряжений
в этот
момент времени будут распределены по синусоидальному закону. Сумма же всех напряжений 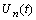 в
любой момент будет равна нулю (Рис.53б), что и показывает справедливость и смысл критерия Найквиста.
в
любой момент будет равна нулю (Рис.53б), что и показывает справедливость и смысл критерия Найквиста.
Из такого представления критерия Найквиста видно значение
условий, накладываемых на систему с ОС, при выводе критерия. Ясно, что невыполнение вышеуказанных
условий в любой степени приводят к недостоверности критерия. В литературе [18,33] приводится причина
неприменимости критерия Найквиста к неминимальнофазовым цепям, подробно также объясняется требование
аналитичности передаточной функции системы. Влияние же нелинейности системы на степень достоверности
критерия в литературе, как правило, не рассматривается. Действительно, критерий был обоснован автором
для абстрактной линейной системы, поведение которой описывается линейными дифференциальными
уравнениями. К нелинейным системам, которыми являются все реальные устройства, он, строго говоря, не
применим.
Однако, на основе опыта приложения линейного анализа к
нелинейным системам без ОС, принято считать, что результаты, полученные при анализе линейных систем,
могут быть применены, хотя и с некоторыми погрешностями, и к реальным, нелинейным устройствам.
Представляет интерес насколько это справедливо в приложении к системам с ОС.
Как было выше показано, фазовые отношения входного
синусоидального сигнала и выходного отличаются в зависимости от того, рассматриваем ли мы их при t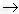 0 или при t
0 или при t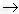
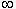 . При t
. При t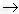 0 входное и выходное синусоидальные
напряжения можно рассматривать как синфазные, тогда как при t
0 входное и выходное синусоидальные
напряжения можно рассматривать как синфазные, тогда как при t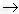
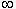 , когда процесс
считается установившимся, между входным и выходным синусоидальными сигналами устанавливается
определённый фазовый сдвиг. Поэтому вывод об устойчивости усилителя, если годограф его передаточной
функции не охватит точку с координатами - (-1,0), полученный Найквистом при t
, когда процесс
считается установившимся, между входным и выходным синусоидальными сигналами устанавливается
определённый фазовый сдвиг. Поэтому вывод об устойчивости усилителя, если годограф его передаточной
функции не охватит точку с координатами - (-1,0), полученный Найквистом при t 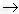
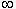 , при t
, при t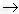 0 может быть не верным.
0 может быть не верным.
Действительно, независимо от фазовых сдвигов в цепях при t = 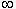 при передаче на вход усилителя с
при передаче на вход усилителя с 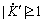 напряжения, процесс нарастания амплитуды
выходного напряжения стремится к бесконечности. Однако нарастание его ограничивается нелинейностью
реальной схемы, причём. Обратная связь при выходе усилителя на нелинейный режим работы разрывается.
напряжения, процесс нарастания амплитуды
выходного напряжения стремится к бесконечности. Однако нарастание его ограничивается нелинейностью
реальной схемы, причём. Обратная связь при выходе усилителя на нелинейный режим работы разрывается.
Иногда в литературе встречается представление, что
неустойчивость характеризуется незатухающими колебаниями. Однако это не всегда так. Иногда
неустойчивость проявляется в том, что под действием внешнего возмущения устройство лавинообразно
переходит в одно из предельных режимов работы - насыщения, или запирания, в котором остаётся до тех пор,
пока очередное воздействие не перебросит его в другой предельный режим работы. Баланс фаз необходимо
учитывать только в применении к автогенераторам с колебательным контуром, с тем, чтобы обеспечить "раскачку"
контура, но и в этом случае допускается значительный диапазон сдвигов фаз.
Таким образом, критерий Найквиста, (как и Михайлова, и Рауса-Гурвица),
несмотря на его математическую безупречность, может не быть верным в приложении к реальным системам с
ОС, так как их поведение значительно отличается от поведения математической модели принятой
Найквистом при выводе своего критерия.
10. Материал, изложенный в настоящей работе, не исчерпывает все
возможности предлагаемого метода. В нём описана, в основном, его сущность, принципы его применения к
различным видам систем с обратными связями, а также отношение описываемого метода к принятым
теоретическим воззрениям на обратную связь. Ряд вопросов, касающихся метода степенного ряда, ещё
требуют теоретической проработки.
Представляет интерес разработать расчётные методики для анализа
и синтеза конкретных реальных устройств с ОС и внедрить описываемый метод в практику машинного
проектирования радиосхем, радиосистем, электронных устройств, устройств автоматического
регулирования и управления и пр.
Метод степенного ряда обладает наглядностью, что позволяет
пользоваться им не только как средством анализа, но и как удобным средством описания процессов
происходящих в устройстве или системе с обратной связью.
ГЛАВА 8. ПРИНЦИПЫ ПОСТРОЕНИЯ СОВРЕМЕННЫХ ИИС
Применение современных средств схемотехники (интегальных
датчиков, микросхем, микропроцессоров и т.д.) коренным образом меняет принципы построения ИИС. Кроме
того, методы достаточно обоснованного определения информационных потоков позволяют существенно
уменьшить их избыточность. Это позволяет поставить задачу о возможно максимальном переносе обработки
измерительной информации к месту её формирования. То есть перейти к конвейерной обработке
измерительной информации в распределённой информационно-измерительной системе. В целом такая система
состоит из следующих основных частей: системы первичных преобразователей (датчиков), устройств сбора и
первичной обработки информации, средств вторичной обработки информации, устройств управления и
контроля, устройств связи с другими системами объекта, накопителей информации. Построение таких систем
в той или иной отрасли человеческой деятельности может существенно отличаться. Мы попытаемся
рассмотреть этот вопрос в области, где требования к аппаратуре наиболее жёсткие. А именно, в области
авиационного и ракетно-космического машиностроения. Естественно, такие системы могут быть применены и
на других мобильных видах техники (автомобилях, судах и т.п.).
Кроме общих требований предъявляемых к ИИС (точность и
достоверность информации), в условиях аэрокосмического применения к ИИС, как и ко всей бортовой
аппаратуре, предъявляются такие требования как:
- минимум весо-габаритных характеристик;
- устойчивость к перегрузкам, ударам, вибрациям;
- устойчивость
работы в условиях интенсивных радиоэлектронных помех;
-
работа в широком диапазоне температур;
- высокая надёжность и
ремонтопригодность;
- высокие эргономические свойства.
Всё это порождает перед разработчиком массу проблем. Надеюсь, что
некоторые идеи, изложенные в настоящей работе, помогут в их решении.
Итак, кратко рассмотрим основные группы технических средств,
входящих в ИИС. К ним можно отнести совокупность первичных преобразователей (датчиков), средства сбора
и первичной обработки информации, средства вторичной обработки, средства управления и контроля,
накопители информации и средства связи с системами объекта.
1. Совокупность первичных преобразователей (датчиков) можно
разделить на три основные группы:
- датчики, в которых никаких других функций, кроме
преобразования входного параметра в электрический сигнал в принципе невозможно, например
тензодатчики;
- датчики, в которых можно разместить некоторые
электронные компоненты, позволяющие формировать тестовые сигналы, хранить данные градуировочных
характеристик и пр.;
- датчики, в которых можно производить
первичную обработку информации, в том числе, такими датчиками могут быть, по сути, другие бортовые
средства и системы, например БЦВМ.
2. Поскольку датчики размещаются по всему объекту, то имеет смысл
группировать их по видам и локализации на объекте и подключать к блокам первичной обработки информации
по радиальной схеме. Сами же блоки, поскольку они позволяют реализовать достаточно сложные протоколы
обмена, объединить между собой и другими вычислительными устройствами системы через параллельный
канал связи, например МАНЧЕСТЕР-2. Таким образом, общую структуру системы можно представить в виде схемы
Рис.54. 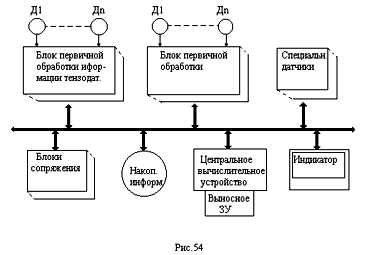
В систему входят:
- блоки первичной обработки информации с датчиков, в которых
какая либо обработка информации не может производиться в принципе, например тензодатчики;
- блоки первичной обработки измерительной информации с датчиков, конструктивное исполнение которых
позволяет производить некоторые функции связанные с обработкой информации;
- специальные датчики. Обычно такие датчики, в которых производится первичная обработка информации и
имеется выход на канал связи в системе;
- блоки сопряжения с
другими источниками информации, например со штатными системами (курсовые системы, инерциальные
системы навигации и т.п.), а также с другими измерительными системами. Кроме того, это могут быть системы
телеметрической связи, а также исполнительные системы (например, системы автоматического управления,
автопилоты и пр.);
- в систему могут входить различные накопители
информации, в том числе аварийные регистраторы;
- информация со
всех источников поступает в центральное вычислительное устройство, в котором производится вторичная
обработка информации, и результаты ее выводятся на устройство индикации, в системы управления объектом,
на телеметрию, накопители и т.п.;
- если ИИС не штатная, то в неё
может входить устройство индикации и управления.
3. Как отмечалось выше, датчики можно классифицировать в виде трёх
групп - тензометрического типа, датчики с встроенными электронными компонентами и специальные датчики.
К датчикам тензометрического типа можно отнести все датчики, в
которых имеется только чувствительный элемент, где под действием измеряемого параметра меняется какая
либо электрическая характеристика (сопротивление, ёмкость, возникает ЭДС и т.д.). Каких либо средств
обработки информации или средств сопряжения с системой в таких датчиках разместить нельзя. Нужно либо
использовать для этих функций отдельный специализированный блок, и тогда это будет по нашей
классификации специализированный датчик, либо, группируя такие датчики (если их много) подключать их к
блоку сбора информации. В целом такой блок будет иметь структуру общую для таких блоков, и отличаться
схемами сопряжения с датчиками. Первичная обработка информации по датчикам тензометрического типа
может производиться на основе паспортных данных на датчики данного типа, имеющих некие средние
статические и динамические характеристики.
Если особенности применения и конструктивные характеристики
датчика позволяют разместить в нём электронные компоненты, то есть основания подумать о том какие
функции эти компоненты могут выполнять. С точки зрения системного подхода было бы желательно, чтобы
замена датчика при его поломке или снятии на тарировку не требовала изменений в математическом
обеспечении ИИС.
В связи с этим, в датчике должна быть репрограммируемое ЗУ с
электрической перезаписью информации небольшого объёма. Туда, в процессе тарировки датчика, с помощью
соответствующих автоматизированных средств, производится запись данных о тарировочной (
градуировочной) характеристике в виде коэффициентов рассчитанным по методикам описанным выше.
Желательно, чтобы в датчике был источник тестового сигнала для
контроля работоспособности датчика.
Датчик должен иметь сопряжение с блоком сбора информации со
стандартизированным протоколом, позволяющим давать команду датчику на выдачу контрольного измерения,
градуировочных данных и текущей информации. Связь желательно осуществлять по однопроводной схеме с
передачей дискретного цифрового кода, что позволяет получить приемлемую защиту от помех.
При достаточной степени стандартизации таких датчиков,
электронные схемы могут выполняться с высокой степенью интеграции, обладать предельно малыми
весогабаритными характеристиками и высокой надёжностью.
Структура такого датчика показана на Рис.55.
|
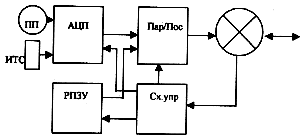
|
|
Рис.55 |
В схему датчика входят: первичный преобразователь и источник
тестового сигнала, подключаемые к аналого-цифровому преобразователю (АЦП), с которого информация
поступает на преобразователь параллельного кода в последовательный, откуда, через схему сопряжения, на
линию связи с блоком сбора информации. Нормальное напряжение на линии связи - высокое. При подаче этого
напряжения от блока сбора информации на датчик, оно, как сигнал, поступает на схему управления. При этом
запускается последовательность работы датчика, при которой в систему передаются тестовый сигнал,
данные градуировочной характеристики, а затем измеряемый параметр.
4. Блоки сбора информации однотипны и могут отличаться схемами
сопряжения с датчиками и программами первичной обработки. Структурная схема такого блока показана на
Рис.56.
Общими для таких блоков являются узел процессора, состоящий из
процессора, ОЗУ и ПЗУ, узел связи с интерфейсом системы и узел питания. Узел связи с датчиками должен
соответствовать особенностям совокупности датчиков, которые к нему подключаются.
Математическое обеспечение процессора, записанное в ПЗУ,
выполняет задачи по осуществлению контроля датчиков, получения от них информации о градуировочных
характеристиках (включая коэффициенты масштабирования), получению информации о текущем значении
параметров, первичной обработке измерительной информации по методикам изложенным выше.
Опрос датчиков производится в соответствии с алгоритмом,
загружаемым от центрального вычислительного устройства, где указываются частоты опроса датчиков,
перечень опрашиваемых датчиков и параметры их первичной обработки.
|
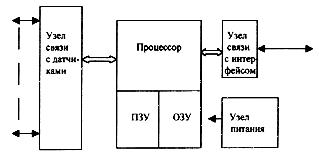
|
|
Рис.56 |
|
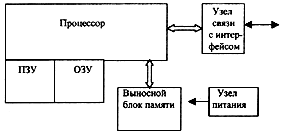
|
|
Рис.57 |
Запросы на получение информации о параметрах поступают от
центрального вычислительного устройства. От него же поступают команды на тестирование датчиков и
самого блока.
5. Центральное вычислительное устройство имеет структуру,
показанную на Рис.57.
Конструктивной особенностью центрального вычислительного
блока является наличие выносного блока памяти. В случае если ИИС разрабатывается как штатная, он может
и отсутствовать, так как математическое обеспечение в этом случае не меняется и может быть полностью
размещено в ПЗУ. Однако если система применяется в условиях, когда задачи, выполняемые ИИС меняются (например
при испытаниях объекта), такой блок необходим.
Выносной блок памяти предназначен для двух целей. Во-первых, в нём
размещается совокупность программ определяющих специфику работы ИИС в условиях конкретного задания.
При этом определяются совокупность измеряемых параметров, режимы их первичной обработки, алгоритмы
вторичной обработки, определяется алгоритм взаимодействия с оператором, перечень фиксируемых
параметров и т.д. В процессе выполнения задания, результаты полной обработки измерений также
записываются в выносной блок памяти. После выполнения задания выносной блок памяти снимается и
поступает для дальнейшей обработки и анализа соответствующим специалистам.
Конструктивно выносной блок памяти может быть изготовлен в виде
блока памяти на цилиндрических магнитных доменах.
ПЗУ центрального вычислительного блока, кроме общих системных
программ, должен иметь в себе комплект математического обеспечения для поддержки вторичной обработки,
в частности программы вычисления трансцендентных функций. Теоретические основы построения таких
программ изложены выше.
6. Кроме описанных блоков, в систему могут входить ряд устройств
согласования со штатными системами объекта, с телеметрией и пр. В теоретическом плане, на наш взгляд,
особых проблем в их разработке проблем не возникает, и на них мы останавливаться не будем.
Отдельный интерес представляет вопрос о конструктивной
реализации индикатора. Особенно если система не является штатной и применяется, например, для
испытаний мобильных объектов (например, летательных аппаратов). В этом случае к индикатору
предъявляются особые требования. Он должен быть малогабаритным и позволять устанавливать его в
различных условиях.
|

|
|
Фото.1 |
|

|
|
Фото.2 |
Примером такого индикатора может быть устройство, показанное на
Фото.1. Он позволяет включать ИИС, производить её контроль в любое время, при помощи переключателя и
кнопки «РЕЖИМ» выбирать нужную программу измерений и обработки. При этом на дисплей выводятся
начальные условия проведения эксперимента. Оператор (лётчик-испытатель) приводит объект в
соответствие заданным условиям и нажимает кнопку «ПУСК». На дисплее индицируются задаваемые текущие
режимы и, после окончания эксперимента, на дисплей выводится информация об успешности или не
успешности эксперимента и (в случае если эксперимент выполнен успешно) обобщенные результаты
вторичной обработки. Далее выбирается следующий режим и т.д.
Способы установки индикатора могут быть различными. В том числе,
может крепиться на бедре лётчика, как показано на Фото.2.
7. Кроме собственно ИИС, для обеспечения её работы необходимы
некоторые вспомогательные системы. В частности, средства для тарировки датчиков, средства
автоматизации подготовки ИИС к конкретным задачам, а также средства автоматического анализа
результатов измерений.
Средства для тарировки датчиков могут создаваться в виде
автоматизированного рабочего места имеющего структуру, показанную на Рис.58.
|
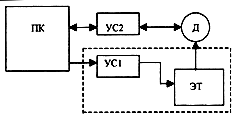
|
|
Рис.58 |
|
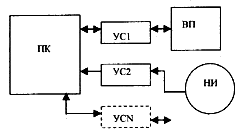
|
|
Рис.59 |
В соответствии с заданной программой тарировки, от персонального
компьютера задаваемая величина эталонного параметра через устройство сопряжения УС1 подаётся и
источник эталонного параметра ЭТ, откуда параметр подаётся на датчик Д. С датчика информация поступает
через устройство сопряжения УС2 в компьютер. После снятия данных по всему диапазону изменения
параметра, данные обрабатываются, и полученные тарировочные коэффициенты записываются в датчик. Для
каждого типа датчика создаются соответствующие математические средства и подсистемы источников
эталонных параметров. Подключение их к компьютеру может производится вручную, а может и при помощи
коммутаторов.
8. Средства подготовки ИИС и автоматизированного анализа
могут быть объединены в виде рабочего места инженера (РМИ). Структура РМИ показана на Рис.59. В него
входят: персональный компьютер ПК, устройство сопряжения с выносной памятью (ВП) УС1, устройство
сопряжения с накопителем информации (НИ) УС2, а также другие необходимые средства (например, средства
связи с телеметрией, со средствами внешнетраекторных измерений и т.п.).
В РМИ формируется соответствующее математическое обеспечение,
включающее в себя: - базу данных об объектах данного вида;
- базу данных о данном типе объекта;
- типовые программы измерений;
- оболочку программирования ИИС;
- программы обработки информации с ВП совместно с информацией с накопителей информации, данных
телеметрии и внешнетраекторных измерений;
- программ
автоматизированного анализа результатов измерений с учетом информации по объектам соответствующих
видов и типов;
- программы подготовки необходимой документации и
т.д.
Оболочка программирования ИИС позволяет выбрать необходимую
совокупность экспериментов, внести в них соответствующие данные (исходные режимы, перечни датчиков,
частоты их опроса и т.д.), записать их в ВП, произвести моделирование (особенно по параметрам связанным с
безопасностью), документально оформить задание на эксперимент и т.д.
9. Описанная структура технических и программных средств ИИС
позволяет весьма существенно сократить сроки и затраты на проведение работ связанных с измерениями.
Это достигается следующим.
Во-первых, объект может быть полностью оборудован всей
совокупностью датчиков и блоков ИИС. В процессе проведения исследований, под каждый эксперимент
совокупность датчиков и программ обработки информации определяется программно. Благодаря этому,
процесс подготовки объекта к проведению экспериментов резко сокращается по времени и трудозатратам.
Во-вторых, процесс проведения измерений и обработки может
производиться одновременно в реальном масштабе времени, что позволяет резко сократить время и
трудозатраты на обработку информации.
В-третьих, совокупность экспериментов выполняемых на данном
этапе проведения работ (например, в данном испытательном полёте) может быть запрограммирована с
некоторой избыточностью. Кроме того, диалоговая форма общения оператора с ИИС позволяет ему достаточно
строго выдерживать параметры эксперимента и знать его результаты. В целом, это позволяет существенно
повысит эффективность работы оператора и максимально качественно выполнить задание, что также
существенно сокращает сроки и затраты на проведение работ.
В-четвёртых, определение частот опросов по выше приведенным
методикам позволяет обеспечить метрологическую обоснованность, а, следовательно, достоверность
результатов измерений.
В-пятых, расчет количества датчиков по методикам, описанным выше (в
частности, тензометрических датчиков), позволяет определить метрологически обоснованное количество
датчиков, что обеспечивает достоверность полученной информации и, возможно, уменьшить их количество до
реально необходимого.
В-шестых, автоматизация процессов подготовки ИИС к
экспериментам, проведения экспериментов и обработки информации в реальном масштабе времени и анализа
после проведения экспериментов обеспечивает возможность сосредоточения всех работ в одних руках,
руках специалиста работающего на РМИ. Это резко сокращает потери времени, обычно возникающие от
несогласованности и от отсутствия взаимопонимания, если в работе участвуют много специалистов. В связи
с этим, имеется возможность резко сократить количество персонала, время на выполнение работ, а
следовательно и затрат на них.
ПРИЛОЖЕНИЕ 1. ОБЗОР ТЕОРЕТИЧЕСКИХ ОСНОВ ДИСКРЕТИЗАЦИИ
Проблема дискретизации широко освещена в литературе. Считается,
что первыми основополагающими работами в этой области были работа Котельникова В.А. [ 1] “О пропускной
способности “эфира” и проволоки в электросвязи”, вышедшая в 1933г. и независимо от него статья “Связь
при наличии шума” [2], написанная К.Шенноном и опубликованная в 1949г. Статья Шеннона была написана на
основе работы Уиттекера “Функции представляемые распространением теории интерполяции”[34] вышедшей в
1915 году, а также [35].
В математическом плане, проблема представления функции её отдельными
значениями и восстановление её при помощи интерполяции начала решаться ещё в 18 веке в работах Лапласа,
Ньютона и т.д.[7]. Бурное развитие теории и практики связи и информации в целом столкнулось с
необходимостью дальнейшего развития методов определения частоты дискретизации, оптимальной
интерполяции и стохастических характеристик дискретизации и интерполяции. Вследствие этого, было
предпринято ряд попыток решить эту проблему как в общем, фундаментальном плане, так и для конкретных
практических приложений.
Появились такие работы, как статья Железнова Н.А. “Исследование
ортогональных разложений стохастических сигналов с неограниченным спектром”[36] вышедшая в 1957г.,
работа Хлистунова В.Н. “Основы цифровой электроизмерительной техники”[37] и т.д.
Появились ряд попыток, так или иначе усовершенствовать основные
методы, например в таких работах, как [38,39,40,41 и т.д.]. Однако практика создания и использования ИИС не даёт
оснований считать, что имеются достаточно простые, удобные и эффективные методы расчёта ИИС.
Критерии определения частоты дискретизации можно сгруппировать
следующим образом:
1. Частотные критерии, при которых частота дискретизации
выбирается с учётом частоты спектра дискретизируемой функции;
2. Корреляционные критерии, устанавливающие связь между
интервалом дискретизации и интервалом автокорреляции функции;
3. Квантовые критерии отсчётов [42] приложимые к детерминированной
модели сигнала и устанавливающей зависимость интервалов между отсчётами от значения ступени
квантования по уровню и крутизне (первой производной) сигнала;
4. Критерий наибольшего отклонения, заключающийся в выборе такого
интервала дискретизации, чтобы разность между функцией с ограниченным числом производных и
полиномом Лангранжа не превышал определённой величины.
1. Частотные критерии основываются на теореме отсчётов. В России
он известен больше как теорема Котельникова (в первоисточнике Теорема II), которая гласит: “Любую
функцию F(t) состоящую из частот от 0 до f1 , можно непрерывно передавать с любой точностью при помощи
чисел следующих друг за другом через 1/2f1 сек.. Действительно, измеряя величину F(t) при t= n/2t1 (n
целое число), мы получим: F(n/2t1) = Dnw1 (8){нумерация формул
по первоисточнику}.
Так как все члены ряда (1) для этого значения f обращаются в нули
кроме члена с k=n, который, как это легко можно получить, раскрывая неопределённость, будет равняться Dnw1. Таким образом, через каждую 1/2f1 сек. мы сможем установить
очередное Dk. Передавая эти Dk по очереди через 1/2f1 сек., мы
сможем по ним согласно ур.(1) почленно восстанавливать F(t) с любой точностью.”
Эта теорема обосновывается Теоремой I, которая гласит: “Любую
функцию F(t), состоящую из частот от 0 до f1 пер. в сек., можно представить рядом: 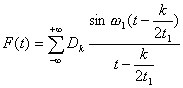 (1),
(1),
Где 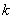 - целое число,
- целое число, 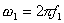 ,
, 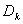 - постоянные зависящие от
- постоянные зависящие от 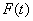 .
.
И наоборот, любая функция 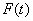 представляемая рядом
(1) состоит лишь из частот от 0 до
представляемая рядом
(1) состоит лишь из частот от 0 до 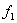 пер. в сек.
пер. в сек.
ДОКАЗАТЕЛЬСТВО {приводится с некоторыми несущественными сокращениями}
Любая функция 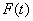 , удовлетворяющая условию Дерихле (конечное число максимумов, минимумов и точек разрыва на любом
конечном отрезке) и интегрируемая в пределах -¥ до +¥, что всегда в
электротехнике имеет место, может быть представлена интегралом Фурье.
, удовлетворяющая условию Дерихле (конечное число максимумов, минимумов и точек разрыва на любом
конечном отрезке) и интегрируемая в пределах -¥ до +¥, что всегда в
электротехнике имеет место, может быть представлена интегралом Фурье.
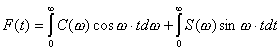 (2).
(2).
Причём:
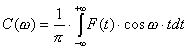 (3),
(3),
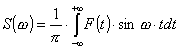
так как 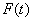 состоит из частот от 0 до
состоит из частот от 0 до 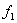 , то
, то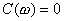 и
и 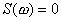 при
при 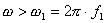 и поэтому
и поэтому 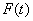 может быть представлена согласно ур.2 так:
может быть представлена согласно ур.2 так:
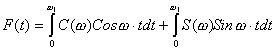 (4)
(4)
Функции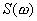 и
и 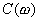 на
участке
на
участке 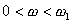 могут быть представлены рядами Фурье, причём эти ряды, по нашему желанию, могут
состоять из одних косинусов или одних синусов, если мы за период возьмём
могут быть представлены рядами Фурье, причём эти ряды, по нашему желанию, могут
состоять из одних косинусов или одних синусов, если мы за период возьмём 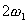 (см. Смирнов – “Курс
высшей математики”, т.II изд.1931г., стр.385[50].)
(см. Смирнов – “Курс
высшей математики”, т.II изд.1931г., стр.385[50].)
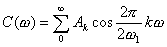 (5а)
(5а)
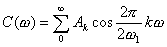 (5б)
(5б)
Введём следующие обозначения:
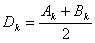 (6)
(6)
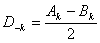 ,
,
тогда формулы (5) можно переписать так:
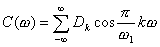 (7)
(7)
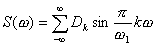
Подставляя (7) в (4), после некоторого преобразования и интегрирования получим ур.(1).”
Теорема Котельникова сыграла значительную роль в развитии
теории связи и информации. Она наглядна при спектральном представлении сигнала. Её преимуществом
является методологический характер. Из неё вытекает не только частота дискретизации, но и метод
восстановления рядом Котельникова и способ восстановления при помощи идеального фильтра.
Однако создание телеметрических устройств поставило вопрос о
точности передачи сигнала. И здесь становится очевидным, что, несмотря на её полезность в применении к
системам связи, к которым метрологические требования не предъявляются, в применении к ИИС она просто не
приемлема, поскольку в этой области проявляются ряд её недостатков. Это вызвало дискуссию и попытки
усовершенствовать эту теорему [и т.д.]. Некоторый итог дискуссии подвёл А.А.Харкевич [43], после чего число
публикаций на эту тему резко снизилось. При этом утвердилось мнение, что теорема Котельникова является
основополагающей теоремой в области теории импульсной связи, которая является, однако, приближённым
утверждением.
В зарубежной литературе теорему отсчётов, аналогичную теореме
Котельникова, принято называть теоремой Шеннона. Она была опубликована в 1949 году в статье “Связь при
наличии шума”. Эта теорема звучит так: “Теорема 1. Если функция не содержит частот выше Wгц, она
полностью определяется своими мгновенными значениями в моменты, отстоящие друг от друга на 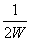 сек.”
сек.”
Доказательство её следующее:
Пусть 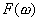 есть спектр
есть спектр 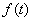 , тогда:
, тогда:
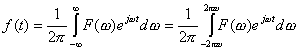 , (2)
, (2)
(нумерация формул по первоисточнику) так как 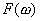 равно нулю вне полосы W.
равно нулю вне полосы W.
Положив 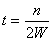 , получим
, получим 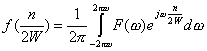
В интервале справа можно узнать n-й коэффициент разложения 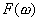 по
гармоникам с периодом от –W до +W , это означает, что отсчёты
по
гармоникам с периодом от –W до +W , это означает, что отсчёты 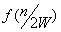 определяют коэффициенты Фурье
в разложении
определяют коэффициенты Фурье
в разложении 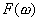 .” Далее доказывается, что функция может быть полностью восстановлена по
отсчётам если применить импульс вида:
.” Далее доказывается, что функция может быть полностью восстановлена по
отсчётам если применить импульс вида: 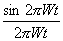 . (6)
. (6)
Тогда 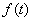 определяется как
определяется как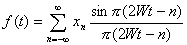 . (7)
. (7)
В своём доказательстве Шеннон ссылается на работу Уиттекера “Теория
интерполяционных функций” вышедшую в 1935г.
Созвучен этим теоремам и так называемый барьер Найквиста.
В современных изданиях приводится, как правило, вывод теоремы
Котельникова по Шеннону [43,44 и т.д.]. Чаще всего теорема Котельникова(Шеннона) приводится вообще без
доказательства [45,46,47.48 и т.д.].
Как упоминалось выше, теореме отсчётов присущи ряд недостатков,
которые не позволяют считать её точной, а следовательно и применимой для метрологической экспертизы
ИИС и их расчёта. Эти недостатки следующие [45,32,3,43,41,47,49 и т.д.]:
- неограниченность спектров реальных сигналов ;
- невозможность создания идеального фильтра;
- сложность расчётов
при восстановлении функции членами ряда Котельникова;
- теорема
не позволяет определять стохастические характеристики погрешностей при дискретизации;
- вносятся дополнительные погрешности за счёт того, что не представляется возможным рассмотреть
выборки на всей оси времени от -¥ до +¥;
- даже при принятии теоремы отсчётов как приближённого утверждения, интервал между отсчётами является
неопределённым, так как граничная частота принимается до некоторой степени произвольно;
- двойственность коэффициентов ряда, которые не могут одновременно обладать значениями функции в
определённые моменты и коэффициентами ряда разложения.
Кроме того, как будет показано в ПРИЛОЖЕНИИ 2, теорема отсчетов не
согласуется со стробоскопическим эффектом.
Есть основания считать, что и вывод теоремы отсчётов не лишен
недостатков. Действительно, в выводе теоремы Котельникова формула 5а опирается на формулу из книги
Смирнова [50] 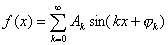 , которая приводится для иллюстрации сущности гармонического разложения. В
дальнейшем она заменена на более точный вид разложения Фурье:
, которая приводится для иллюстрации сущности гармонического разложения. В
дальнейшем она заменена на более точный вид разложения Фурье:
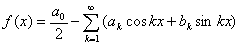 , которая приводится во всех источниках по гармоническому анализу [51,5,11,52,53,54 и т.д.].
Причём, как правило, подчёркивается особое место коэффициента
, которая приводится во всех источниках по гармоническому анализу [51,5,11,52,53,54 и т.д.].
Причём, как правило, подчёркивается особое место коэффициента
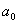 . Например [51]: “… необходимо,
однако, ещё раз подчеркнуть особое положение параметра
. Например [51]: “… необходимо,
однако, ещё раз подчеркнуть особое положение параметра 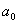 , входящего в разложение лишь своей половиной”. Введение же в формулу 5а половины
постоянной составляющей делает невозможным дальнейшее преобразование и вывод теоремы в целом.
, входящего в разложение лишь своей половиной”. Введение же в формулу 5а половины
постоянной составляющей делает невозможным дальнейшее преобразование и вывод теоремы в целом.
Что касается вывода теоремы по Шеннону (Уиттеккеру), то здесь
сказывается упомянутая двойственность коэффициентов ряда. По существу вывод заключается в повторном
применении ряда Фурье к действительной функции 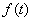 . При первом преобразовании получается
спектр
. При первом преобразовании получается
спектр 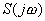 , состоящей из двух составляющих – АЧХ и ФЧХ. Применение интеграла Фурье к
, состоящей из двух составляющих – АЧХ и ФЧХ. Применение интеграла Фурье к 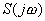 должно выражаться в виде интегрирования по Фурье его действительной и мнимой части как
действительных функций, что приведёт уже к четырём переменным. Следовательно, интеграл Фурье от
должно выражаться в виде интегрирования по Фурье его действительной и мнимой части как
действительных функций, что приведёт уже к четырём переменным. Следовательно, интеграл Фурье от 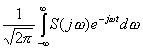 может быть взят в виде:
может быть взят в виде: 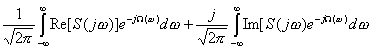 , что также делает вывод теоремы отсчётов по Шеннону
невозможным.
, что также делает вывод теоремы отсчётов по Шеннону
невозможным.
Действительно, 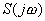 есть комплексная переменная,
интеграл от которой берётся на плоскости, то есть по двум переменным. Это подтверждается также тем, что
имея набор равноотстоящих отсчётов от некоторой синусоиды, по этим отсчётам можно восстановить
бесконечное число синусоид [55]. Исходя из вышеизложенного можно понять причину по которой исходя из
теоремы отсчетов рекомендуется выбирать частоту опросов F0³(3¸10)Fmax а
иногда и больше, причём рекомендаций по определению Fmax как правило не даётся.
есть комплексная переменная,
интеграл от которой берётся на плоскости, то есть по двум переменным. Это подтверждается также тем, что
имея набор равноотстоящих отсчётов от некоторой синусоиды, по этим отсчётам можно восстановить
бесконечное число синусоид [55]. Исходя из вышеизложенного можно понять причину по которой исходя из
теоремы отсчетов рекомендуется выбирать частоту опросов F0³(3¸10)Fmax а
иногда и больше, причём рекомендаций по определению Fmax как правило не даётся.
2.Корреляционный критерий был предложен Н.А.Железновым
в работе[36] “Исследование ортогональных разложений стохастических сигналов с неограниченным спектром”,
опубликованной в 1957г.
Сущность метода заключается в том, что интервал между отсчётами
определяется по величине автокорреляционной функции сигнала. Преимущество метода заключается в том,
что он распространяется на сигналы имеющие неограниченный спектр. К недостаткам можно отнести:
- применимость его только к стационарным сигналам, так как для
нестационарных сигналов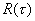 не является стационарной величиной, а, следовательно, DТ,
рассчитанная для средней
не является стационарной величиной, а, следовательно, DТ,
рассчитанная для средней 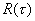 , будет приводить к ошибке при более высокой динамичности
процесса;
, будет приводить к ошибке при более высокой динамичности
процесса;
- определение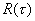 представляет собой довольно
сложную задачу и требует больших вычислительных работ, а также наличия реализации процесса, что при
разработке ИИС, как правило, невозможно;
представляет собой довольно
сложную задачу и требует больших вычислительных работ, а также наличия реализации процесса, что при
разработке ИИС, как правило, невозможно;
- из критерия не следует
стохастические характеристики процесса дискретизации;
-
критерий не определяет оптимальной интерполяции.
Метод Железнова близок к методу Котельникова, поскольку спектр и
автокорреляционная функция связаны формулой Винера-Хинчина [45]. С этой точки зрения критерий Железнова
более общий, в то время как теорема Котельникова описывает сингулярные процессы [45,56], которые, вообще
говоря, информации не несут.
В связи с перечисленными недостатками метод Железнова не явился
методологической базой при определении частоты дискретизации в ИИС, хотя в области связи этот метод
достаточно эффективен.
3. Квантовый критерий отсчётов [42] при равномерной интерполяции
приводит к неравномерной дискретизации, и рассматриваться здесь не будет.
4.Сущность метода определения частоты дискретизации по критерию
наибольшего отклонения заключается в том, что в нём реализуется интерполяционный подход [3,48,37,5747].
Используется интерполяционный полином Лагранжа в виде:
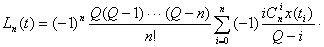 ,
,
где 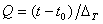 ;
; 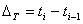 ,
, 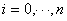 .
.
Погрешности интерполяции полиномами Лагранжа 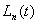 непрерывной
функции
непрерывной
функции 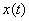 , которая имеет на отрезке
, которая имеет на отрезке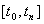 ограниченные производные порядка
ограниченные производные порядка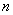 , определяются остаточным членом:
, определяются остаточным членом:
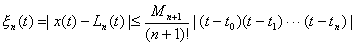 , где
, где 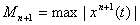 .
.
Отсюда, из условия 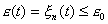 , где
, где 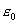 - заданная
допустимая погрешность дискретизации, определяется
- заданная
допустимая погрешность дискретизации, определяется 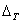 .
.
Например, для 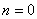 ,
, 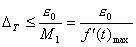 ;
;
для 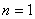 ,
, 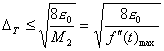 ;
;
в общем случае: 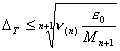 ,
,
где 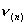 коэффициент зависящий от
коэффициент зависящий от 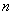 и
и 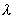 , где
, где 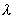 - показатель
качества приближения.
- показатель
качества приближения.
Главным преимуществом этого метода является то, что он связывает
непосредственно интервал между отсчетами, допустимую погрешность и показатель динамики функции –
максимальное значение производной функции.
Недостатками являются следующие:
- метод не позволяет определить стохастические характеристики
дискретизации;
- не определяется оптимальная степень
интерполирующего полинома;
- метод не точен в отношении функции
дифференцируемой до бесконечности.
6.Кроме приведенных методов имеются и другие [38,39,58], которые
являются вариантами рассмотренных выше методов. Известен метод[57,59] определения частоты дискретизации
по среднеквадратическому отклонению. Метод требует определения автокорреляционной функции и
стационарности процесса. Близок методу Железнова.
В работе[38] приведен метод, который использует подход по методу
наибольшего отклонения и подходы, применяемые в частотных критериях. В целом ему присущи недостатки
как стохастических, так и частотных методов.
Предпринимались попытки [39] определить интервал дискретизации с
применением различных полиномов Лагранжа, с использованием стохастических свойств функции в виде
автокорреляционной функции. Как и предыдущие работы не вносит существенной новизны и обладает тем
недостатком, что не определяет оптимальной интерполяции, требует стационарности процесса, а также
другими недостатками методического плана.
Таким образом, обзор существующих методов показывает, что к
настоящему времени в известной литературе не приводится методов обоснования частоты дискретизации, её
стохастических характеристик и связанной с ней интерполяции и экстраполяции, достаточно эффективных
для определения характеристик ИИС.
ПРИЛОЖЕНИЕ 2. СТРОБОСКОПИЧЕСКИЙ ЭФФЕКТ
Стробоскопический эффект в теории измерительной информации
недостаточно известен. В связи с этим рассмотрим его подробнее. Применение здесь частотных методов
здесь весьма затруднительно. В работе [60] приведена попытка решения этой задачи. Здесь исходная функция
представлена в виде последовательности отсчётов умноженных на ряд равноотстоящих d-функций.При
этом результирующая функция приобретает вид:
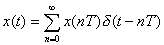 , где
, где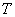 - период дискретизации,
- период дискретизации, 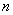 - номер отсчёта. В результате
довольно громоздких выкладок показано, что “спектр квантованной величины оказался отличным от нуля и
на низких частотах, хотя этих частот в непрерывной функции не содержалось”. В общепринятом понимании
теоремы Котельникова(Шеннона) появления новых спектральных составляющих быть не должно, поскольку это
искажение сигнала.
- номер отсчёта. В результате
довольно громоздких выкладок показано, что “спектр квантованной величины оказался отличным от нуля и
на низких частотах, хотя этих частот в непрерывной функции не содержалось”. В общепринятом понимании
теоремы Котельникова(Шеннона) появления новых спектральных составляющих быть не должно, поскольку это
искажение сигнала.
|
|
|
Рис.60 |
В связи с этим, остановимся на рассмотрении стробоскопического
эффекта. Дана исходная синусоида. Из неё сделаны выборки с частотой несколько большей удвоенной
частоты синусоиды. Далее функция восстанавливается фильтром. В результате получается модуляция с
некоторой частотой W. Этот процесс промоделирован на установке, схема которой
показанаРис.60.
В состав установки входят: генератор синусоидальных
колебаний (ГСК); формирователь синхроимпульсов (ФСИ); модулятор (М); генератор импульсов (ГИ); фильтр (Ф) и
осциллограф. Фильтр - низкочастотный с прямоугольной полосой пропускания. Генератор импульсов - с
регулируемой скважностью.
В результате исследования стробоскопического эффекта получены осциллограммы,
показанные на приведенных ниже фотографиях.
|

|
|
Фото.3 |
|

|
|
Фото.4 |
|

|
|
Фото.5 |
|
|
|
Фото.6 |
|

|
|
Фото.7 |
|

|
|
Фото.8 |
|

|
|
Фото.9 |
|
|
|
Фото.10 |
|

|
|
Фото.11 |
На Фото.3 показана исходная синусоида. На Фото.4 полученные выборки,
частота которых несколько больше удвоенной частоты синусоиды. На Фото.5 – сигнал, полученный после
восстанавливающего фильтра. Явно видно возникновение биений на частоте примерно на 8% больше удвоенной
частоты синусоиды. При повышении частоты выборок в пределах одной кратности частота биений
увеличивается (Фото.6 и Фото.10). А при увеличении кратности частоты выборок по отношению к частоте
синусоиды амплитуда биений уменьшается (Фото.7 и Фото.11). При достаточно большой кратности (Фото.8,9),
восстановленная синусоида визуально становится неотличимой от исходной синусоиды (Фото.3).
Очевидно, что если частота выборок равна удвоенной частоте
синусоиды, то, в зависимости от фазового сдвига, выборки могут попадать на нулевые значения синусоиды,
экстремумы или промежуточные значения. В связи с этим, поскольку априорно фаза выборок относительно
синусоиды нам не известна, то после восстановления сигнала фильтром синусоиду вообще можно не
увидеть. Поэтому можно сказать, что погрешность в передаче синусоиды при частоте выборок равной
удвоенной частоте синусоиды равна ста процентам. Уже этого достаточно для подтверждения правильности
выводов изложенных во второй главе.
Тем не менее, произведем некоторые теоретические исследования
этого эффекта. Итак, дана исходная синусоида с частотой 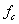 . Из неё делаются выборки с
частотой
. Из неё делаются выборки с
частотой 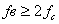 . При этом используется полосовой фильтр низких частот с частотой среза
. При этом используется полосовой фильтр низких частот с частотой среза 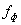 несколько большей
несколько большей 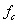 . В результате, если частота выборок несколько больше
удвоенной частоте синусоиды, то после фильтра синусоида оказывается модулированной другой
низкочастотной синусоидой с частотой W. Расстояние между узлами биений определяется
набегом фазы между выборками и синусоидой. При этом каждый узел соответствует совпадению выборки с
нулём синусоиды. В этом случае, сдвиг на p/2 получается за
. В результате, если частота выборок несколько больше
удвоенной частоте синусоиды, то после фильтра синусоида оказывается модулированной другой
низкочастотной синусоидой с частотой W. Расстояние между узлами биений определяется
набегом фазы между выборками и синусоидой. При этом каждый узел соответствует совпадению выборки с
нулём синусоиды. В этом случае, сдвиг на p/2 получается за 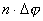 , где
, где 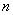 - число выборок, а
- число выборок, а 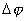 - разность фаз между выборками и полупериодов синусоиды.
Но разность фаз может быть сведена к разности частот. Отсюда частота биений W равна -
- разность фаз между выборками и полупериодов синусоиды.
Но разность фаз может быть сведена к разности частот. Отсюда частота биений W равна - 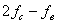 .
.
Можно выбрать такие соотношения 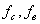 и
и 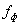 , что составляющие спектра биений окажутся в области полосы пропускания фильтра настолько,
что взаимовлиянием спектра кратных частот выборок можно пренебречь. В этих условиях соблюдение
требований теоремы Котельникова налицо в полном объёме. При этом проявляется двойственность, в
спектральном представлении процесса. С одной стороны, результат восстановления синусоиды на фильтре
можно представить в виде биения двух близких по частоте и равных по амплитуде синусоид, что не совсем
верно поскольку несущая частота восстановленного сигнала следует за частотой выборок и непонятно
совпадение амплитуд при неравномерности АЧХ фильтра, или модуляцией довольно сложной и богатой в
спектральном отношении функцией. Это более соответствует действительности, учитывая нелинейность
преобразования. Действительно, через счётное число точек можно провести бесконечное число как
синусоид, так и функций вообще. Фильтр “не знает” ЧЕГО ОТ НЕГО ЖДУТ. Он просто выбирает такую функцию,
которая бы требовала минимума энергии по принципу наименьшего действия [61].
, что составляющие спектра биений окажутся в области полосы пропускания фильтра настолько,
что взаимовлиянием спектра кратных частот выборок можно пренебречь. В этих условиях соблюдение
требований теоремы Котельникова налицо в полном объёме. При этом проявляется двойственность, в
спектральном представлении процесса. С одной стороны, результат восстановления синусоиды на фильтре
можно представить в виде биения двух близких по частоте и равных по амплитуде синусоид, что не совсем
верно поскольку несущая частота восстановленного сигнала следует за частотой выборок и непонятно
совпадение амплитуд при неравномерности АЧХ фильтра, или модуляцией довольно сложной и богатой в
спектральном отношении функцией. Это более соответствует действительности, учитывая нелинейность
преобразования. Действительно, через счётное число точек можно провести бесконечное число как
синусоид, так и функций вообще. Фильтр “не знает” ЧЕГО ОТ НЕГО ЖДУТ. Он просто выбирает такую функцию,
которая бы требовала минимума энергии по принципу наименьшего действия [61].
При частотах выборок кратных частоте синусоиды и больших 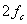 также наблюдаются биения. При этом наблюдается принцип суперпозиции. Например, при
также наблюдаются биения. При этом наблюдается принцип суперпозиции. Например, при 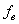 »
» 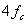 процесс можно представить в виде совместного действия двух
частот опроса со сдвигом на DT/2. Очевидно, что наибольшая амплитуда биения будет в момент
равноотстоящий от двух пучностей. Поскольку огибающие биений – синусоиды, то амплитуда биений равна
процесс можно представить в виде совместного действия двух
частот опроса со сдвигом на DT/2. Очевидно, что наибольшая амплитуда биения будет в момент
равноотстоящий от двух пучностей. Поскольку огибающие биений – синусоиды, то амплитуда биений равна 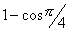 . Несложно показать, что число 4 есть отношение
. Несложно показать, что число 4 есть отношение 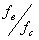 .
.
Аналогично можно получить такие же соотношения для
любых кратностей частот выборок и синусоиды. Общая формула будет иметь вид: 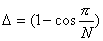 , где
, где 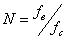 . (П2.1)
. (П2.1)
|
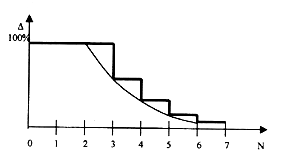
|
|
Рис.61 |
Вообще говоря, отношение частот выборок и синусоиды не целое число.
За счёт этого зависимость погрешности от соотношения частот выборок и синусоиды несколько усложняется,
но эти тонкости уже выходят за рамки настоящей работы. Графически эта зависимость показана на Рис.61.
ПРИЛОЖЕНИЕ 3. ТОЧНОСТЬ КОСИНУСОИДАЛЬНОЙ АППРОКСИМАЦИИ
|
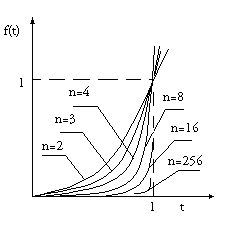
|
|
Рис.62 |
Известно, что всякую аналитическую функцию можно представить в
виде степенного полинома [60]: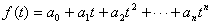 .
.
В частном случае можно рассмотреть идеальную модель, при которой 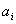 , при
, при 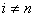 , равно нулю, а при
, равно нулю, а при 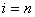 равно единице. При этом,
равно единице. При этом, 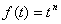 . Совокупность таких функций показана на Рис.62. Кривизна функции выражается формулой[5]
. Совокупность таких функций показана на Рис.62. Кривизна функции выражается формулой[5] 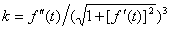 .
.
В общем случае: 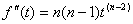 ,
, 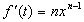 ;
;
Тогда
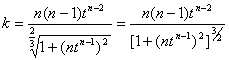 .
(П3.1)
.
(П3.1)
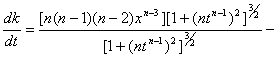
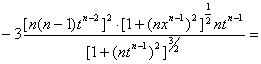
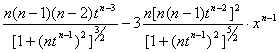 . (П3.1)
. (П3.1)
Экстремум 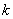 определяется при
определяется при 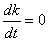 . Тогда,
приравняв это выражение к нулю и упростив, можно получить:
. Тогда,
приравняв это выражение к нулю и упростив, можно получить: 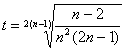 .
.
Подставив полученное 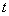 в (П3.1)
можно получить:
в (П3.1)
можно получить: 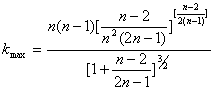 .
.
Графически эта функция будет иметь вид, показанный
на Рис.63:
|
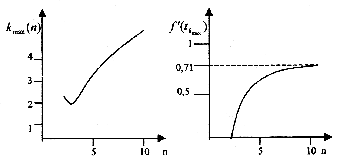
|
|
Рис.63
Рис.64 |
Для определения интервалов опросов необходимо развернуть
функции  таким образом, чтобы переменная
таким образом, чтобы переменная 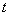 была нормальна к
вектору
была нормальна к
вектору 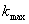 . В точках
. В точках 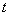 , соответствующих
, соответствующих 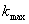 линия, перпендикулярная
вектору совпадает с
линия, перпендикулярная
вектору совпадает с 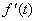 . Общее выражение в этом случае:
. Общее выражение в этом случае: 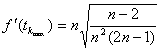 . Графически эта
зависимость показана на Рис.64.
. Графически эта
зависимость показана на Рис.64.
Далее, для сравнения этих функций по интервалам дискретизации
необходимо их нормализовать к r=1. Это достигается уменьшением кривизны функции за счёт
увеличения масштаба 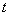 . При нормальном положении оси времени к вектору
. При нормальном положении оси времени к вектору 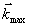 ,
, 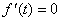 . Тогда
. Тогда 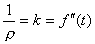 .
.
Если ввести масштаб 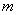 по
по 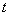 , то
, то 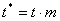 (П3.2), тогда
(П3.2), тогда 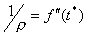 . При
. При 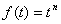 ,
, 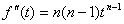 . С учетом (П3.2),
. С учетом (П3.2), 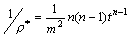 . Таким образом, при
. Таким образом, при 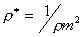 получается переход к уравнению:
получается переход к уравнению: 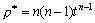 . То есть, для
нормализации
. То есть, для
нормализации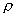 на
на 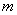 необходимо увеличить
необходимо увеличить 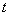 в
в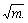 раз.
Используя вышеприведенные соображения, были произведены расчёты на ЭВМ, в результате которых получены
результаты отражённые на Рис.65.
раз.
Используя вышеприведенные соображения, были произведены расчёты на ЭВМ, в результате которых получены
результаты отражённые на Рис.65.
|
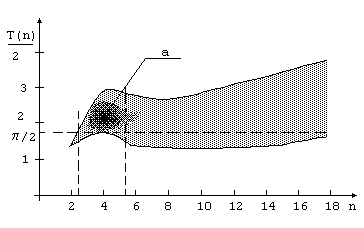
|
|
Рис.65 |
По оси n отложена степень составляющей степенного полинома. По оси
ординат половина интервала дискретизации. Поскольку кривая нормированной степенной функции
несимметрична, то мы имеем две кривые, определяющие максимальную и минимальную величину полупериода
дискретизации. На рисунке отражена величина полупериода дискретизации определяемая по методу
косинусоидальной аппроксимации - 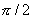 . Из рисунка видно, требуемые интервалы
дискретизации, исходя из анализа измеряемого параметра как степенного ряда, в целом больше, чем
определяемые по методу косинусоидальной аппроксимации. При этом нужно учитывать, что реальный
параметр практически никогда не состоит из одной степенной функции. Причем, чем выше степень члена
степенного ряда, тем меньше его коэффициент
. Из рисунка видно, требуемые интервалы
дискретизации, исходя из анализа измеряемого параметра как степенного ряда, в целом больше, чем
определяемые по методу косинусоидальной аппроксимации. При этом нужно учитывать, что реальный
параметр практически никогда не состоит из одной степенной функции. Причем, чем выше степень члена
степенного ряда, тем меньше его коэффициент 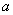 , то есть меньше его влияние. В связи с этим,
сумма ряда реального измеряемого параметра определяет такие интервалы дискретизации, которые
находятся в зоне (а) показанной на рисунке.
, то есть меньше его влияние. В связи с этим,
сумма ряда реального измеряемого параметра определяет такие интервалы дискретизации, которые
находятся в зоне (а) показанной на рисунке.
Таким образом, мы можем сделать вывод, что определение интервалов
дискретизации по методу косинусоидальной аппроксимации, во-первых, является достаточно точным, во-вторых,
практически безизбыточно.
В отдельных, практически редких случаях, когда параметр близок
квадратичной функции, может потребоваться несколько большая частота измерений. Для этого случая в
совокупность формул расчета частоты опроса введена соответствующая формула.
Кроме того, нужно учитывать и то, что при метрологическом расчёте
измерительной цепи, погрешность дискретизации должна определяться исходя из принципа ничтожной
малости, при этом сама погрешность в определении частоты дискретизации является величиной второго
порядка малости и ею, в данном случае можно пренебречь.
Можно высказать и более общие соображения в пользу
косинусоидальной аппроксимации. Просмотр материалов реальных измерений создаёт определённое
впечатление, что многие из них, особенно в наиболее –динамичной части, тяготеют к синусоидальному виду.
И это не случайно. Объектами измерений, как правило, являются гомеостатическими системами
поддерживающими своё заданное состояние или изменяющее его по заданному закону. Это состояние
определяется совокупностью обратных связей. Реакция таких систем на возмущающее воздействие
описывается уравнениями, дающими или апериодические, или колебательные решения, которые в своей
совокупности порождают переходные характеристики хорошо аппроксимирующиеся отрезками синусоиды.
ПРИЛОЖЕНИЕ 4. ОБЗОР И АНАЛИЗ МЕТОДОВ ИНТЕРПОЛЯЦИИ
Задача интерполяции неразрывно связана с задачей дискретизации.
Интерполяция в явном или неявном виде проводится всегда. В явном виде интерполяция производится в том
случае, когда параметры, необходимые для расчёта характеристик, измеряются с разной частотой, а
характеристики вычисляются с частотой равной максимальной частоте опроса из частот опрашиваемых
параметров. Кроме того, интерполяция производится в ряде случаев при графическом представлении
параметров или характеристик. При этом интерполяция реализуется программно или аппаратно. В неявном
виде интерполяция производится в том случае, если информация регистрируется в табличном виде и
интерполяцию производят сознательно или бессознательно, производя оценку значений функции между
замерами.
1.Проблема интерполяции давно привлекала математическую мысль [7].
Великие математики CVII столетия были хорошо знакомы с методами равноотстоящей
интерполяции полиномами и развили теорию конечных разностей до высокого уровня. Они пользовались
обыкновенными, а также центральными разностями. Основополагающая работа Грегори (1638-1679) была
продолжена Ньютоном. Стирлинг, а позднее Бессель добавили ещё несколько формул. Строгая разработка
теории интерполяции начинается с Гана и Фихера. Опасности, связанные с равноотстоящим
интерполированием полиномами были обнаружены независимо друг от друга Рунге (1904) и Борелем (1903).
Разработка методов интерполяции при помощи ортогональных функций была разработана Фурье,
Остроградским, Уиттекером, Котельниковым. Методы интерполяции дискретных последовательностей
разрабатывались Уолшем, Хааром и т.д.
В последнее время большую известность получили метод сплайн-функций,
разработанный в 1948г. [62,63 и т.д.]. Кроме того, к вопросам интерполяции можно отнести метод Гаусса (метод
наименьших квадратов). Разрабатывались стохастические методы интерполяции [45].
В целом, известные методы интерполяции можно разделить на три
основных группы:
- методы с применением степенных рядов;
- методы с применением ортогональных функций;
- методы
стохастического анализа.
2.Сущность методов степенных рядов заключается в предположении,
что исходная (до дискретизации) функция может быть представлена степенным рядов вида: 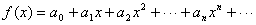 при
при
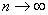 . Если предположить, что
. Если предположить, что 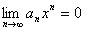 , что обычно выполняется, то
, что обычно выполняется, то 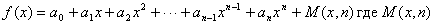 сумма
остальных членов ряда.
сумма
остальных членов ряда.
Тогда: 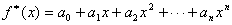 будет интерполирующий ряд.
будет интерполирующий ряд.
Для определения ряда 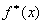 необходимо определить
необходимо определить 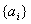 , для чего нужно решить систему уравнений при известных значениях
, для чего нужно решить систему уравнений при известных значениях 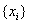 . Способы
определения
. Способы
определения 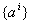 , по известным
, по известным 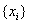 , бывают различными, что и определяет различие
методов интерполяции полиномами.
, бывают различными, что и определяет различие
методов интерполяции полиномами.
Одним из наиболее известных интерполяционных алгебраических
полиномов является полином Лагранжа [3,48,45 и т.д.]. Известные разновидности полинома Лагранжа –
интерполяционные формулы Ньютона, Гаусса, Бесселя, Стирлинга, Эферетта, сплайн-функции и др.
Преимуществом методов степенных полиномов является их
простота при реализации на ЭВМ, поэтому сейчас они являются основными при обработке информации на ЭВМ.
Недостатками методов степенных полиномов являются появление эффекта увеличения погрешности при
увеличении степени полинома [7] и недостаточная обоснованность применения их к случайным функциям. Это
связано с тем, что методы интерполяции первоначально разрабатывались для потребностей астрономии, в
частности для расчёта параметров орбит небесных тел (планет, комет, спутников и т.д.) и для составления
астрономических календарей. В этих случаях кривая движения небесных тел описывалась с достаточной
точностью конечными степенными полиномами, например, движение тела вокруг планеты без спутников
описывается кривой второго порядка. Таким образом, интерполирующий полином будет также конечным,
конечным является и необходимое число замеров.
Кроме того, методы интерполяции степенными полиномами нашли
применение там, где описывающие полиномы заранее известны и их надо восстановить по известным
значениям в отдельных точках. Такая задача решается, например, в чертёжных автоматах.
Что же касается случайных функций, то интерполяция конечными
полиномами связана с погрешностями, которые существенно влияют не только на качество восстановления
функции, но и на саму возможность применять интерполяцию для восстановления исходной функции.
3. Методы применения ортогональных разложений начали развиваться
со времени разработки разложения функций по синусоидальным составляющим, разработку которого
связывают с именем французского математика Фурье. Математическое значение разложения периодических
функций в ряд по синусоидальным функциям было осознано в XVII веке Эйлером и Лагранжем. Заслугой Фурье
было распространение возможностей такого разложения на неаналитические функции. Теория ортогональных
функций была широко рассмотрена русским математиком Остроградским М.В. [64]. Он отмечал, что “ряд 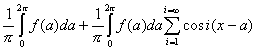 является одним из наиболее простых и полезных рядов, охватываемых общим разложением.”
Синусоидальные разложения нашли широкое применение в связи с развитием радиосвязи. Их эффективность
оказалась столь высока, что многие начали считать спектральные составляющие сигнала реально
существующими [65.66]. В связи с дискретной передачей, в качестве интерполирующей функции В.А.Котельниковым
был предложен ряд ортогональных функций вида:
является одним из наиболее простых и полезных рядов, охватываемых общим разложением.”
Синусоидальные разложения нашли широкое применение в связи с развитием радиосвязи. Их эффективность
оказалась столь высока, что многие начали считать спектральные составляющие сигнала реально
существующими [65.66]. В связи с дискретной передачей, в качестве интерполирующей функции В.А.Котельниковым
был предложен ряд ортогональных функций вида: 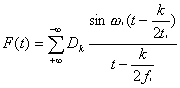 .
.
Ортогональными функциями являются функции Чебышева и т.д.
Применение этих методов в практике измерений не нашло широкого применения при обработке измерительной
информации в связи со сложностью связанных с ними расчётов.
4.Методы стохастического анализа в своей сущности состоят в
определении математического ожидания погрешности дискретизации. В настоящее время при
метрологическом анализе процесса дискретизации чаще всего идут этим путём (например [45] и др.). Эти
методы пока не нашли широкого применения вследствие трудностей определения стохастических
характеристик исходной информации. Кроме того, эти методы применимы для стационарных случайных
процессов, в то время, как реально измеряемые параметры таковыми, как правило, не являются. Хотя
методически эти методы более приемлемы, так как они отражают случайный характер измеряемой информации.
Таким образом, несмотря на обилие методов интерполяции, до
настоящего времени вопрос о выборе оптимального метода интерполяции в приложении к обработке
измерительной информации до конца не решён.
ЗАКЛЮЧЕНИЕ
Итак, уважаемые коллеги, всё что я хотел нужным изложить
относительно теории технической информации, я изложил. Конечно, что то осталось по разным соображениям
не включённым в эту книгу. В частности, некоторые вопросы конструктивно-технологического характера, а
также материалы апробации разработанных методик и конструктивных решений. Если кого-то заинтересуют
эти вопросы, могут ко мне обратиться.
Заранее хочу ответить тем критикам, которые скажут, что
теоретический аппарат изложенных в книге методик слишком прост. Моё мнение таково, что попытки
применять без особой на то необходимости какие-то последние писки математической моды редко приводят к
чему-либо путному. Иногда думают, что стоит найти какую-то волшебную формулу, и все проблемы разрешатся.
Так не бывает. Чаще бывает наоборот.
Действительно, реальные процессы в природе сложны. Мало того, они
до конца человеческому разуму не постижимы. В лучшем случае мы формируем в своём сознании некоторую
модель, которая в какой-то мере может соответствовать физическому процессу. Для математического
описания такую модель часто приходится настолько упрощать, что, даже если математический аппарат
разработан безукоризненно, получаемые выводы могут совершенно не соответствовать действительности.
Примером такого, на мой взгляд, недопустимого, упрощения является ограничения накладываемые на систему
с ОС Найквистом.
А иногда некоторые авторы просто занимаются
математическим украшательством. В связи с этим уместно привести мнение по этому вопросу известного
математика, академика Л. Понтрягина [67]: «В последнее время опасным становятся математические
спекуляции в теоретической физике и технических науках. Дело доходит до того, что серьёзная работа в
области техники может быть ошельмована на том основании, что в ней нет математических обоснований, хотя
всем может быть ясна практическая пригодность исследований. Для математика обидно, что иногда её
привлекают для бутафории., для того, чтобы спрятать бедность и немощность той или иной специальной
работы .... Высокий уровень абстракции современной математики способен гипнотизировать тех, кто не
является в ней специалистом, и, очевидно, порождает в их среде досужее мнение, неверное представление,
особое почтение лишь к кабалистическим формулировкам и недоверие к ясности и простоте действительно
научных утверждений.»
Тем не менее я готов с благодарностью принять конструктивную
критику, предложения и пожелания, которые конечно будут отражены в следующих изданиях книги, если
таковые последуют.
Материал, изложенный в книге, был готов лет десять
назад. Но, в связи с известными событиями в стране, не удалось его в полном объёме реализовать как в
практике измерительных работ, так и в публикациях. Тем не менее, апробация результатов теоретических
исследований и ряда конструктивных решений была проведена при выполнении ряда работ в области
испытаний авиатехники. Материалы теоретических исследований были доложены в ряде научных организаций,
таких как ВВИА им. проф. Жуковского, на семинарах общества Попова и пр. Имеются публикации (к сожалению
не очень доступные). Каких либо серьёзных замечаний научная общественность не высказывала.
Вполне возможно, что кто-то из моих уважаемых коллег пришёл к
результатам аналогичным изложенным в этой книге. Я не хотел бы ввязываться в дрязги связанные с
приоритетом. Поэтому, если мне будут представлены соответствующие материалы, в последующих изданиях
они будут включены в книгу, или на них будут сделаны соответствующие ссылки.
Имеются ряд вопросов, которые не рассмотрены в книге. Например,
вопросы, связанные со статистическим анализом измеряемых параметров и состава датчиков, вопросы
стандартизации и унификации, перспективных конструкторско-технологических решений на базе
современной схемотехники и системотехники и пр. Думаю, что было бы полезным в рамках творческого
коллектива подготовить более объёмную книгу.
Думаю, что в настоящее время можно поставить вопрос о создании
базовой концепции построения ИИС с разработкой стандартизованных и унифицированных требований к
интерфейсам (в частности интерфейсу связи с датчиками), программным оболочкам и пр. В этом случае, фирмы,
выполнившие эту работу, имеют шанс выйти в лидеры не только в область ИИС, но и в области датчиков. То
есть, создать себе условия аналогичные тем, которые обеспечили, скажем, успех фирме Microsoft. Тем более, что
рынок для такой аппаратуры может быть очень широкий.
Специалистам в области ИИС вряд ли нужно перечислять сферы
применения теории и технических средств информационно-измерительной техники. Тем не менее, для тех, кто
больше связан с организацией и управлением производством, вкратце подскажу некоторые из них:
- аэрокосмическая техника (штатное и испытательное оборудование);
- наземная мобильная
техника (автомобили, железные дороги и пр., штатное и испытательное оборудование);
- надводные и
подводные суда и корабли;
- метеорологические системы и системы мониторинга, в том числе космического;
-
промышленные установки (ректификационные колонны, химические и биологические реакторы и пр.);
-
энергетика (ядерные реакторы, котлы и т.д.)
- биотелеметрия и т.д.
Во всех этих областях применения, методические и технические
средства, разработанные с учётом изложенных в этой книге материалов, обеспечат высокую степень
достоверности измерений, их метрологическую обоснованность, снижение затрат на разработку аппаратуры
и её эксплуатацию, сокращение сроков испытаний и т.д. А следовательно и немалые материальные выгоды.
Например, при проведении космического мониторинга, исходя из
необходимой точности измерений, обосновывается количество и орбиты спутников Земли. Естественно, если
это обоснование достаточно корректно, то количество спутников может быть оптимально. Если же не
корректно, то число их может быть либо меньше необходимого (при этом снижается достоверность
информации, а, следовательно, и её ценность и, конечно, стоимость). Либо больше, и тогда будут большими
затраты на создание спутниковой системы. А что изготовление и запуск даже одного спутника стоит очень
дорого, известно всем. И для того чтобы сэкономить эти средства нужно просто просчитать их необходимое
число с помощью методик, основанных на изложенном в этой книге материале.
(Сайт "ЧРЕЗ ТЕРНИИ К ЗВЕЗДАМ".Григоренко А.М.)
Copyright©2001
СПИСОК ЛИТЕРАТУРЫ
1. Котельников В.А. О пропускной способности «эфира» и проволоки в электросвязи. -
ВЭК,1933.
2. Шеннон К. Работы по теории информации и кибернетике. - М.: Издательство иностранной литературы,
1963.
3. Темников Ф.Е., Афонин В.А.,Дмитриев В.И. Технические основы информационной техники. - М.: Энергия,1979.
4.
Широков К.П., Довбета Л.И. О понятиях «измерительная система» и «измерительная информационная система».
«Измерительная техника».№5,1980.
5. Корн Г. и Т. Справочник по математике. – М.: Наука,1977.
6. Чувыкин В.В.
Способ оценки погрешности восстановления функций, представленными дискретными значениями. «Цифровая
инф.изм. техника».– Пенза: №10,1980.
7. Ланцош К. Практические методы прикладного анализа. – М.: Физматгиз,
1961.
8. Березин И.С., Житков Н.П. Методика вычислений. Т.1,2. – М.: Физматгиз,1960.
9. Методический материал по
применению ГОСТ 8.009-72. ВНИИМС. – М.: Изд. Стандартов, 1975.
10. Новицкий П.В. Об особых свойствах 95% - ной
квантили большого класса распределений и предпочтительных значениях доверительной вероятности при
указании погрешностей приборов и измерений. Метрология, №2, 1979.
11. Гоноровский И.С. Радиотехнические
цепи и сигналы. – М.: Соврадио,1977.
12. Отнес Р., Эноксон А. Прикладной анализ временных рядов. – М.: Мир, 1982.
13.
Браммер К., Зифменг Г. Фильтр Калмана-Бьюси. – М.: Наука, 1982.
14. Горовец А.М. Синтез систем с обратной
связью. – М.: Советское радио, 1970.
15. Waldhauer F.D. Feedback – cjnceptual or physical? Simp. on circuit theory. IEEE Cat ND73CH0765-8CT. Toronto. 1973. P8-12
16.
Трохименко Я.К. Ошибки формальной теории усилителей с обратной связью. Изв.ВУЗов. Радиоэлектроника. 1973.
Т.16.№2.
17. Основы автоматического управления. Под ред. В.С.Пугачёва.
18. Г.Боде. Теория цепей и
проектирование усилителей с обратной связью. – М.: Изд. ин.лит.,1948.
19. Атабеков Г.И. Теоретические основы
электротехники. Ч.1. – М.Л.: Госэнергоиздат. 1962.
20. Шидловский А.К. Взаимность и обратимость в активных и
многофазных электрических цепях. – Киев. 1969.
21. Артым А.Д. Усилители с обратной связью, анализ и
синтез. – Ленинград.: Энергия, 1969.
22. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.:
Наука,1973.
23. Бессекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука,1975.
24.
Кугушев А.М., Голубева Н.С. Основы радиоэлектроники. – М.: Энергия,1969.
25. Скотт Э. Волны в активных и
нелинейных средах в приложении к электронике. – М.: Сов.радио,1977.
26. European conference on circuit theory and design. London, 1974.
27.
Бессонов Л.А. Линейные электрические цепи. – М.: Высшая школа, 1974.
28. Импульсные цепи на
полупроводниковых приборах, проектирование и расчёт. Под ред. Гальперина Е.И. и Степаненко И.П. – М.: Сов.радио,1970.
29.
Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Сов. Радио,1963.
30. Техническая кибернетика. Под
ред. Солодовникова В.В. – М.: Машиностроение,1967.
31. Егоров К.В. Основы теории автоматического
регулирования. – М.: Энергия,1967.
32. Van Valkenburg M.E. Circuit theory: foundations and classical contributions. Strasbourg, 1974.
33. Касьяненко А.А.
Частотные методы устойчивости автоматических систем управления. – Таганрог, 1977.
34. Whittaker J.N. On the function
which are represented by expansions of the interpolation theory. Proc. Roy. Soc. Edinburg. Wol.35, 1915.
35. Whittaker J.N. Interpolatory functions theory. Cambridge. Tract.33 in
Mathematics and Mathematical Physics. Camb. №4, 1935.
36. Железнов Н.А. Исследование ортогональных разложений стохастических
сигналов с пограничным спектром. Труды ЛКВВИА. Вып.191, 1957.
37. Хлистунов В.И. Основы цифровой
электроизмерительной техники. – М.: Энергия, 1966.
38. Ицкович Э.Л. Определение необходимой частоты
измерений при дискретном контроле. Автоматика и телемеханика. Том XXII, 1961.
39. Авербух Г.Ю., Каташков Э.С.,
Розов Ю.Л. Определение максимальной частоты опроса при аналого-дискретном преобразовании. Изм.техника.№3,
1973.
40. Турбович И.Т. К вопросу о применении теоремы Котельникова к функции времени с неограниченным
спектром. Радиотехника №13, 1958.
41. Немировский М.С. Некоторые вопросы разложения функций в ряд по
Котельникову и специфические искажения при использовании амплитудо-импульсной модуляции. Сборник
трудов НИИ. Вып. 5(19), 1956.
42. Темников Ф.Е. Теория развёртывающих систем. – М.Л.: Госэнергоиздат, 1963.
43.
Харкевич А.А. О теореме Котельникова. Радиотехника №8, 1958.
44. Харкевич А.А. Очерки общей теории связи. –
М.: Гостехиздат, 1955.
45. Кавалеров Г.И., Мандельштамм С.М. Введение в информационную теорию измерений. – М.:
Энергия, 1974.
46. Куппершмидт Я.А. Точность телеизмерений. – М.: Энергия, 1978.
47. Малов В.С., Куппершмидт Я.А.
Телеизмерения. – М.6 Энергия, 1975.
48. Орнатский П.П. Теоретические основы информационной измерительной
техники. – Киев. Выща школа, 1976.
49. Мановцев А.П. Основы радиотелеметрии. – М.: Энергия, 1973.
50. Смирнов В.И.
Курс высшей математики. Т.2. – М.Л. ОГИЗ Гостехтздат, 1848.
51. Воробьёв И.Н. Теория рядов. – М.: Наука,1971
52.
Толстов Г.П. Ряды Фурье. – М.: Физматгиз,1965.
53. Кручкович Г.И. Ряды Фурье. Интеграл Фурье. Векторный
анализ. – М.: Физматгиз, 1965.
54. Математические основы современной электроники. Под ред. Гуткина Л.С. – М.:
Соврадио, 1968.
55. Никольс М.Х., Раух Л.А. Радиотелеметрия. – М.: Изд. иностр. лит., 1958.
56. Колмогоров А.Н.
Стационарные последовательности в гильбертовом пространстве. Бюллетень ГГУ 2,6, 1941.
57. Френке А.В.
Телеизмерения. – М.: Высшая школа,1975.
58. Турбович И.Т. Метод близких систем. – М.: Изд. АН СССР, 1961.
59.
Промышленная телемеханика. Под ред. Сотскова Б.С. и Малова В.С. – М.Л.: Энергия, 1966.
60. Фельдбаум А.А.,
Бутковский А.Г. Методы теории управления. – М.: Наука,1971.
61. Фейнман Р., Лейтон Р., Сендс М. Фейнмановские
лекции по физике. – М.: Мир, 1977.
62. Ефимов А.В., Золотарёв Ю.Г., Терпигорова В.Н. Математический анализ (специальные
разделы). Т.2. – М.: Высшая школа. 1980.
63. Стечкин С.В., Субботин Ю.Н. Сплайны и вычислительная математика. –
М.: Наука, 1976.
64. Остроградский М.В. Полное собрание трудов. – Киев: АН УССР, 1959.
65. Финк Л.М. Сигналы,
помехи, ошибки …. – М.: Связь, 1978.
66. Андре Анго. Математика для электро и радиоинженеров. – М.6 Наука,1965.
67.
Понтрягин Л. О математике и качестве её преподавания. Коммунист №14, 1980.
![]() ( 2. 1 ),
( 2. 1 ), ![]() . Обычно считают Ро заданной и в соответствии с [ 4 ] ее можно принять 0.05. В этих условиях
задаются величины только
. Обычно считают Ро заданной и в соответствии с [ 4 ] ее можно принять 0.05. В этих условиях
задаются величины только
![]() , которые в практических случаях
выражаются , как правило, приведенными к максимальной величине диапазона измерения в процентах.
, которые в практических случаях
выражаются , как правило, приведенными к максимальной величине диапазона измерения в процентах.![]() ( 2.2. )
( 2.2. )![]() |f"(t)max|.
|f"(t)max|.
![]() 0 . Следовательно, в
окрестности t0 F(t) является аппроксимирующей функцией. В связи с этим, метод назван методом
аппроксимирующей косинусоиды.
0 . Следовательно, в
окрестности t0 F(t) является аппроксимирующей функцией. В связи с этим, метод назван методом
аппроксимирующей косинусоиды.![]() t +
t +
![]() ). Так как t0 принимается за начало отсчета и при этом F(t) максимально, то
). Так как t0 принимается за начало отсчета и при этом F(t) максимально, то
![]() =0. Тогда F(t) = cos
=0. Тогда F(t) = cos![]() t.
t.![]() 2 cos
2 cos![]() t то |f"(t)max | =
t то |f"(t)max | =
![]() 2 cos
2 cos![]() t.
t.![]() 2 .
2 .![]() 2 = |f"(t)max|
, следовательно:
2 = |f"(t)max|
, следовательно:
![]() =
=![]() | f"(t)max | .
| f"(t)max | .![]() |f"(t)max|)
|f"(t)max|)
![]() t)
.
t)
.![]() д, тогда:
д, тогда:![]() д
д
![]() cos
cos![]() t ; F"(t)max =
t ; F"(t)max =
![]() д
д
![]()
![]() 2 = | f"(t)max | .
2 = | f"(t)max | .![]() =
=
![]() ( | f"(t)max | ) /
( | f"(t)max | ) /
![]() д .
д .![]() д
д
![]() cos{[
cos{[![]() (|f"(t)|max)/
(|f"(t)|max)/![]() д ]
д ]
![]() t } .
(2.3)
t } .
(2.3)![]() а.к./2p =
а.к./2p =
![]() а.к/p .
а.к/p .![]()
![]() | f"(t)max | /
| f"(t)max | /![]() д .
(2.4)
д .
(2.4) ![]()
![]() | f"(t)max | /(
| f"(t)max | /(![]() д
д![]() A)
A)![]() 3
3![]() | f"(t)max | /(
| f"(t)max | /(![]() д
д![]() A) ,
(2.5) где fд - частота дискретизации,
A) ,
(2.5) где fд - частота дискретизации,
![]() д - приведенная
погрешность дискретизации в процентах, A - диапазон измерения.
д - приведенная
погрешность дискретизации в процентах, A - диапазон измерения.![]() [(5-1)
[(5-1)
![]() 9.8]/(0.5
9.8]/(0.5
![]() 10000)
10000)![]() 0.3гц.
0.3гц.![]() 1+[f'(t)]2)3,где k - кривизна функции f(t).
1+[f'(t)]2)3,где k - кривизна функции f(t).![]() , где
, где
![]() - радиус кривизны, то
- радиус кривизны, то![]()
![]() min
min
![]()
![]() д
д
![]() А .
(2.6)
А .
(2.6) ![]()
![]() 0, в точке t = t0 и масштаб времени выбран таким образом, что угол касательных к
аппроксимирующей косинусоиде в точках ее максимальных первых производных (точках перегиба) -
0, в точке t = t0 и масштаб времени выбран таким образом, что угол касательных к
аппроксимирующей косинусоиде в точках ее максимальных первых производных (точках перегиба) - ![]() =
=
![]() /4 , то окрестности точки максимальной
кривизны будут представлять излом функции с углом
/4 , то окрестности точки максимальной
кривизны будут представлять излом функции с углом
![]() /2. Диапазон от
точки излома до линии (a,b) выбирается равным погрешности дискретизации -
/2. Диапазон от
точки излома до линии (a,b) выбирается равным погрешности дискретизации -
![]() д, в котором поведение функции может быть любым. В том числе, она может быть и косинусоидой с
таким периодом, что в точках a и b она имеет своими касательными линии максимальной крутизны.
д, в котором поведение функции может быть любым. В том числе, она может быть и косинусоидой с
таким периодом, что в точках a и b она имеет своими касательными линии максимальной крутизны.
![]() )
)![]() д. Если подставить в
формулу (2.4 ) полученную величину
д. Если подставить в
формулу (2.4 ) полученную величину
![]() = |f"(t)max|, то
= |f"(t)max|, то![]() )
)![]() 1/
1/![]()
![]() д
д![]() (2/
(2/![]() )
)![]()
![]() д , а также
учитывая, что величину погрешности Dд надо также умножить на величину
2/
д , а также
учитывая, что величину погрешности Dд надо также умножить на величину
2/![]() ,
,![]() )
)![]() 1/
1/![]()
![]() 2 ( 4/
2 ( 4/![]() 2) = 1/2
2) = 1/2![]() .
(2.7)
.
(2.7)
![]() д. Отсюда t2
- t1 = 2
д. Отсюда t2
- t1 = 2![]() д и, в свою очередь, fд=1/2
д и, в свою очередь, fд=1/2![]() .
Но было бы желательно делать вывод из общих позиций. Последний же вывод лишний раз показывает
правильность описанного метода.
.
Но было бы желательно делать вывод из общих позиций. Последний же вывод лишний раз показывает
правильность описанного метода.![]() дA. Учитывая, что масштаб
времени t выбран специально для вывода формулы (2.7), и то, что частота опросов меняется линейно с
изменением масштаба времени, а также то, что
дA. Учитывая, что масштаб
времени t выбран специально для вывода формулы (2.7), и то, что частота опросов меняется линейно с
изменением масштаба времени, а также то, что
![]() x/
x/![]() t = tg x, можно написать: fд = 50tg(
t = tg x, можно написать: fд = 50tg(![]() max) /
max) /
![]() дA, или fд = 50f'(t)max /
дA, или fд = 50f'(t)max /
![]() дA. (2.8) Полученные формулы эффективны
при
дA. (2.8) Полученные формулы эффективны
при
![]()
![]()
![]() , в случае
, в случае
![]() >
> ![]() эти формулы дадут завышенное значение fд. Можно меняя масштаб времени t,
обеспечить выполнение условия
эти формулы дадут завышенное значение fд. Можно меняя масштаб времени t,
обеспечить выполнение условия
![]()
![]()
![]() , при этом формула (2.8) приобретет
вид:
, при этом формула (2.8) приобретет
вид:![]() max /
max /
![]() дA , где М
- масштаб времени.
дA , где М
- масштаб времени.![]() )fс arc cos(1 -
)fс arc cos(1 -
![]() д).
(2.9)
д).
(2.9) ![]() )arc cos(1-
)arc cos(1-![]() д/100).
Эта формула может применяться к параметрам имеющим явно выраженный колебательный характер. Например,
колебания элементов конструкции летательного аппарата.
д/100).
Эта формула может применяться к параметрам имеющим явно выраженный колебательный характер. Например,
колебания элементов конструкции летательного аппарата.![]() |f"(t)max| /
|f"(t)max| /
![]() дA (2.10) применяется к параметрам,
получение величины максимальной второй производной в отношении которых не представляет больших
затруднений.
дA (2.10) применяется к параметрам,
получение величины максимальной второй производной в отношении которых не представляет больших
затруднений.![]()
![]()
![]() дA , (2.11)
применяется тогда, когда возможно геометрическое построение зависимости параметра от времени. В
частности, тогда, когда имеется хотя бы одна реализация параметра в его наиболее динамичном виде, (
например записи опробования двигателя ).Кроме того, эта формула может применяться при расчете
количества точек замера по пространственной координате, например количество тензодатчиков по размаху
крыла, При этом строится эпюра механических напряжений и по ее кривизне определяется интервал между
датчиками.
дA , (2.11)
применяется тогда, когда возможно геометрическое построение зависимости параметра от времени. В
частности, тогда, когда имеется хотя бы одна реализация параметра в его наиболее динамичном виде, (
например записи опробования двигателя ).Кроме того, эта формула может применяться при расчете
количества точек замера по пространственной координате, например количество тензодатчиков по размаху
крыла, При этом строится эпюра механических напряжений и по ее кривизне определяется интервал между
датчиками.![]() max /
max /![]() дA (2.12)
применяется в отношении параметров имеющих
дA (2.12)
применяется в отношении параметров имеющих
![]() < Dд, и графическое представление которых достаточно просто. Например, отклонение органов
управления летательного аппарата, которое может регистрироваться на земле. Эта формула может также
применяться в случае
< Dд, и графическое представление которых достаточно просто. Например, отклонение органов
управления летательного аппарата, которое может регистрироваться на земле. Эта формула может также
применяться в случае
![]() > Dд. В этом
случае применяется коэффициент М по шкале времени и формула приобретает вид: f=M50tg
> Dд. В этом
случае применяется коэффициент М по шкале времени и формула приобретает вид: f=M50tg![]() max/
max/![]() A .
A .![]() дA (2.13) применяется в отношении
параметров, для которых более предпочтительным является использование первой производной. Например,
скорости. Однако нужно иметь в виду, что данная формула может дать завышенное значение частоты опросов.
дA (2.13) применяется в отношении
параметров, для которых более предпочтительным является использование первой производной. Например,
скорости. Однако нужно иметь в виду, что данная формула может дать завышенное значение частоты опросов.![]() |f"(t)max| /
|f"(t)max| /
![]() дA .
дA .![]() .
Действительно, никакая физическая величина не может изменить свое значение мгновенно. Изменение
параметра на
.
Действительно, никакая физическая величина не может изменить свое значение мгновенно. Изменение
параметра на
![]() сопряжено с некоторым
сопряжено с некоторым
![]() t. Причем, интервал между отсчетами Т должен быть равным
t. Причем, интервал между отсчетами Т должен быть равным
![]() t,
поскольку при условии Т>
t,
поскольку при условии Т>![]() t увеличится погрешность выше допустимой, а
при T<
t увеличится погрешность выше допустимой, а
при T<![]() t замеры ti+1 и ti становятся коррелированы а,
следовательно, информационно избыточны. При Т=
t замеры ti+1 и ti становятся коррелированы а,
следовательно, информационно избыточны. При Т=
![]() t отсчеты становятся
не коррелированы. Неопределенность величины f(t) к точке ti+1 пределами ±
t отсчеты становятся
не коррелированы. Неопределенность величины f(t) к точке ti+1 пределами ±![]() . То есть можно сказать, что при Т =
. То есть можно сказать, что при Т =
![]() t, отсчеты в пределах ±
t, отсчеты в пределах ±![]() становятся цепью Маркова, или, в более общем понимании, мартингалом.
Естественно, что знание значений f(t) в прошлом ничего не может дать в определении f(t) на
Отсюда станономами выше первой
степени ( то b>i - n), где n = 1,2, . . .), является бессмысленным. В этом и суть
появляющихся ошибок при полиномиальной интерполяции с увеличением степени полинома [7].
становятся цепью Маркова, или, в более общем понимании, мартингалом.
Естественно, что знание значений f(t) в прошлом ничего не может дать в определении f(t) на
Отсюда станономами выше первой
степени ( то b>i - n), где n = 1,2, . . .), является бессмысленным. В этом и суть
появляющихся ошибок при полиномиальной интерполяции с увеличением степени полинома [7].![]() принимается за 0 ), t=
принимается за 0 ), t=![]() /2. Отсюда: (a
/2. Отсюда: (a![]() /2)2=1. Тогда: a2
/2)2=1. Тогда: a2![]() 2=4 ; a=2/p; следовательно f(t)=(2t/
2=4 ; a=2/p; следовательно f(t)=(2t/![]() )2. При f(t)=2, t=
)2. При f(t)=2, t=![]() /
/![]() 2 ,
2 , ![]() /
/![]() 2-
2-![]() /2»
/2»![]() ´0,208. Поскольку
полупериод косинусоиды (он же интервал отсчетов) равен
´0,208. Поскольку
полупериод косинусоиды (он же интервал отсчетов) равен ![]() , то отношение
, то отношение
![]() /
/![]() ´0,208
´0,208![]() 4,8 дает
отношение требуемой частоты дискретизации при экстраполяции по отношению к частоте дискретизации при
интерполяции. Таким образом, частота экстраполяции должна быть выше частоты интерполяции почти в пять
раз. С другой стороны, функция f(t) может быть после точки
4,8 дает
отношение требуемой частоты дискретизации при экстраполяции по отношению к частоте дискретизации при
интерполяции. Таким образом, частота экстраполяции должна быть выше частоты интерполяции почти в пять
раз. С другой стороны, функция f(t) может быть после точки ![]() /2 и
синусоидальной.
/2 и
синусоидальной.
![]() необходимо
и достаточно уменьшить величину интервала вдвое, то есть увеличить частоту дискретизации
вдвое. Таким образом, для случая экстраполяции нужно формулы (2.9,2.10,2.11) умножить на 3, а формулы (2.12,2.13) на 2.
необходимо
и достаточно уменьшить величину интервала вдвое, то есть увеличить частоту дискретизации
вдвое. Таким образом, для случая экстраполяции нужно формулы (2.9,2.10,2.11) умножить на 3, а формулы (2.12,2.13) на 2.







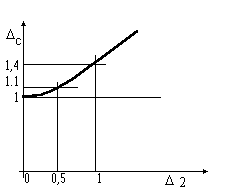










 Аномальные
измерения могут следовать в виде единичных измерений (Рис.26а), пачек или пакетов (б), или в виде разрывов
в измерении параметра (в). Первый может быть связан, например, со сбоями в цифровой аппаратуре, второй с
нарушение контактов в потенциометрических датчиках или пропадание напряжения питания, третий,
например, со склейкой различных участков магнитной ленты регистраторов. Выбор решения в таких случаях
требует адаптивного подхода, который в наибольшей степени свойственен логике человеческого мышления.
Аномальные
измерения могут следовать в виде единичных измерений (Рис.26а), пачек или пакетов (б), или в виде разрывов
в измерении параметра (в). Первый может быть связан, например, со сбоями в цифровой аппаратуре, второй с
нарушение контактов в потенциометрических датчиках или пропадание напряжения питания, третий,
например, со склейкой различных участков магнитной ленты регистраторов. Выбор решения в таких случаях
требует адаптивного подхода, который в наибольшей степени свойственен логике человеческого мышления.
 :
: Очевидно, что этот метод, будучи довольно простым, имеет тот недостаток, что теряется информация в
случае разрывов функции. Попытаемся устранить этот недостаток. Чтобы восстановить функцию после ее
последующего анализа необходимо запоминание её предыдущих значений. Положим, что мы имеем такую память.
Тут могут быть два случая. Во-первых, аномальное измерение представленное рядом выборок, число которых,
тем не менее, меньше чем позволяют динамические характеристики объекта. То есть после последнего
аномального отсчета появляется истинный отсчет, который по отношению к аномальному выглядит как
аномальное измерение. В этом случае каждое очередное измерение проверяется по критерию аномальности,
Когда наступит скачек, все предыдущие аномальные измерения отбрасываются и заменяются линейной
интерполяцией. Если через заданное число измерений нового скачка не наступает, то считается, что это
разрыв функции и все предыдущие аномальные измерения считаются верными и передаются на обработку.
Восстановленная функция при этом будет иметь вид (Рис.29). Однако, как отмечалось, в этом случае
необходима большая оперативная память, а также необходима задержка на обработку, которая может быть
недопустима в случае, если обработка информации должна производится в реальном масштабе времени.
Очевидно, что этот метод, будучи довольно простым, имеет тот недостаток, что теряется информация в
случае разрывов функции. Попытаемся устранить этот недостаток. Чтобы восстановить функцию после ее
последующего анализа необходимо запоминание её предыдущих значений. Положим, что мы имеем такую память.
Тут могут быть два случая. Во-первых, аномальное измерение представленное рядом выборок, число которых,
тем не менее, меньше чем позволяют динамические характеристики объекта. То есть после последнего
аномального отсчета появляется истинный отсчет, который по отношению к аномальному выглядит как
аномальное измерение. В этом случае каждое очередное измерение проверяется по критерию аномальности,
Когда наступит скачек, все предыдущие аномальные измерения отбрасываются и заменяются линейной
интерполяцией. Если через заданное число измерений нового скачка не наступает, то считается, что это
разрыв функции и все предыдущие аномальные измерения считаются верными и передаются на обработку.
Восстановленная функция при этом будет иметь вид (Рис.29). Однако, как отмечалось, в этом случае
необходима большая оперативная память, а также необходима задержка на обработку, которая может быть
недопустима в случае, если обработка информации должна производится в реальном масштабе времени.

 Имеем критерий -
Имеем критерий -
 Таким
образом, в целом алгоритм фильтрации и удаления аномальных измерений может выполняться как одно целое
в виде отдельных блоков, комбинация которых и выбор критериев могут быть различными. Поскольку
переработка алгоритма для каждого случая весьма трудоёмка, то имеет смысл в начале алгоритма иметь
слово описывающее состояние его. В этом случае могут быть идентификаторы, определяющие наличие тех, или
иных критериев, Эти слова могут храниться в самой программе и вызов их может определяться
идентификаторами параметра.
Таким
образом, в целом алгоритм фильтрации и удаления аномальных измерений может выполняться как одно целое
в виде отдельных блоков, комбинация которых и выбор критериев могут быть различными. Поскольку
переработка алгоритма для каждого случая весьма трудоёмка, то имеет смысл в начале алгоритма иметь
слово описывающее состояние его. В этом случае могут быть идентификаторы, определяющие наличие тех, или
иных критериев, Эти слова могут храниться в самой программе и вызов их может определяться
идентификаторами параметра.













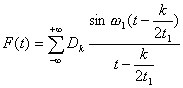 (1),
(1),
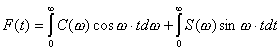 (2).
(2).
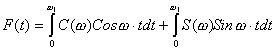 (4)
(4)
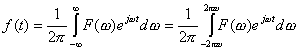 , (2)
, (2)
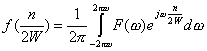
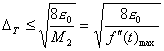 ;
;
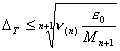 ,
,

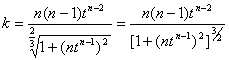 .
(П3.1)
.
(П3.1)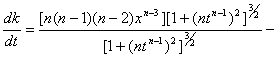
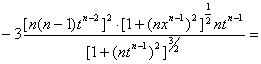
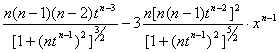 . (П3.1)
. (П3.1)
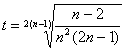 .
.
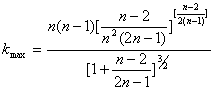 .
.
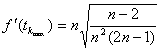 . Графически эта
зависимость показана на Рис.64.
. Графически эта
зависимость показана на Рис.64.

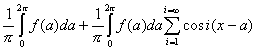 является одним из наиболее простых и полезных рядов, охватываемых общим разложением.”
Синусоидальные разложения нашли широкое применение в связи с развитием радиосвязи. Их эффективность
оказалась столь высока, что многие начали считать спектральные составляющие сигнала реально
существующими [65.66]. В связи с дискретной передачей, в качестве интерполирующей функции В.А.Котельниковым
был предложен ряд ортогональных функций вида:
является одним из наиболее простых и полезных рядов, охватываемых общим разложением.”
Синусоидальные разложения нашли широкое применение в связи с развитием радиосвязи. Их эффективность
оказалась столь высока, что многие начали считать спектральные составляющие сигнала реально
существующими [65.66]. В связи с дискретной передачей, в качестве интерполирующей функции В.А.Котельниковым
был предложен ряд ортогональных функций вида: 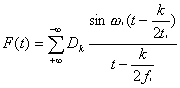 .
.





