1. Математическая теория солнечных календарей и их точность
Календарный год должен содержать целое число суток: либо 365, либо 366. Поэтому для согласования календарного года с тропическим необходимо через определенное число простых лет, содержащих 365 дней, вводить високосные годы в 366 дней. Конечно, невозможно сразу сказать, как часто и в какой последовательности должны быть расставлены простые и високосные годы, чтобы средняя продолжительность года как можно ближе была равна длине тропического года.
Длину тропического года выше мы приняли равной 365,24220 средних солнечных суток (всего на 0,1 секунды больше ее действительной величины!). Следовательно, простой год в 365 дней окажется более коротким на 0,24220 суток. Представим эту десятичную дробь в виде простой дроби: 24220/100000 или 1211/5000. Это значит, что расхождение за 5000 лет составит 1211 суток. Для того чтобы среднюю продолжительность календарного года приблизить к продолжительности тропического года, надо за эти 5000 лет в календарный счет ввести 1211 високосных лет.
Чтобы не связывать исправления календаря со столь длительным промежутком времени, попытаемся представить дробь 1211/5000 другой дробью, у которой числитель и знаменатель будут меньшими, но сама дробь будет по своей величине близка к дроби 1211/5000.
Для решения поставленной задачи воспользуемся способом последовательного деления, известным в теории чисел под названием алгоритма Евклида. Способ последовательного деления дает возможность правильную дробь представить в виде цепной (или непрерывной) дроби. При этом числовые значения последовательно получаемых дробей называются подходящими дробями. Точное значение цепной дроби всегда находится между двумя соседними подходящими дробями, причем оно ближе к последующей, чем к предыдущей подходящей дроби.
Найдем несколько последовательных подходящих дробей K1,K2,K3,... Для отыскания первой подходящей дроби K1 надо числитель и знаменатель дроби разделить на числитель и представить ее в таком виде:
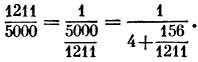
Если пренебречь дробью 156/1211, то первая подходящая дробь K1 будет равна 1/4 или в десятичных знаках (с точностью до пятого знака после запятой) 0,25000.
Полученная нами в результате первого приближения подходящая дробь отличается от дроби 0,24220 на величину 0,00780. Эта разность еще слишком велика. Поэтому продолжим наши расчеты и попытаемся найти подходящую дробь K2, которая будет меньше отличаться от дроби 0,24220.
Для этого с отброшенной выше дробью 156/1211 поступаем таким же образом: делим числитель и знаменатель на числитель. Тогда искомая дробь примет вид
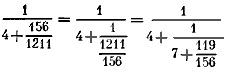 .
.
Если пренебречь дробью 119/156, то вторая подходящая дробь K2 будет равна
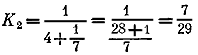 ,
или
в десятичных знаках K2
= 0,24138.
,
или
в десятичных знаках K2
= 0,24138.
Эта подходящая дробь отличается от дроби 0,24220 всего на величину 0,00082.
Продолжим далее наши вычисления и найдем третью подходящую дробь K3 :
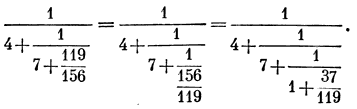
Если пренебречь дробью 37/119, то третья подходящая дробь K3 будет равна
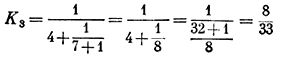 или
в десятичных знаках
или
в десятичных знаках
K3 = 0,24242.
Эта подходящая дробь отличается от дроби 0,24220 на еще меньшую величину: 0,00022.
Найдем четвертую подходящую дробь K4:
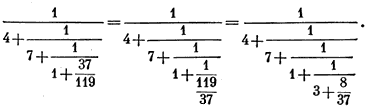
Пренебрегаем дробью 8/37 и находим значение четвертой подходящей дроби:
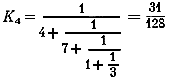 или
в десятичных знаках K4
= 0,24219.
или
в десятичных знаках K4
= 0,24219.
Эта величина отличается от исходной дроби всего на 0,00001 средних солнечных суток, т. е. менее чем на 1 сек.
Мы могли бы вполне ограничиться четырьмя полученными подходящими дробями, так как дальнейшие приближения к величине тропического года не имеют практического смысла. Однако мы найдем еще одну подходящую дробь K5, для того, чтобы показать, что ее численное значение в точности равно той части суток, которой недостает для принятого нами значения тропического года.
Для этого придется использовать отброшенную дробь 8/37. Тогда пятая подходящая дробь примет вид
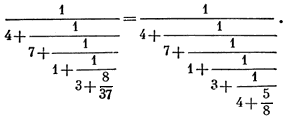
Пренебрегая дробью 5/8, найдем значение пятой подходящей дроби: K5 = 132/545 или в десятичных знаках K5 = 0,24220.
Теперь выпишем все полученные нами подходящие дроби и сопоставим их с принятой величиной 0,24220:
| Разность | |
| K3 = 1/4 = 0,25000 | + 0,00780 |
| K3 = 7/29 = 0,24138 | - 0,00082 |
| K3 = 8/33 = 0,24242 | + 0,00022 |
| K3 = 31/128 = 0,24219 | - 0,00001 |
| K3 = 132/545 = 0,24220 | + 0,00000 |
Из этой таблицы видно, что полученные нами подходящие дроби получаются последовательно то большими, то меньшими, чем выбранная дробь 0,24220, но они все время колеблются около нее и приближаются к ней по своей абсолютной величине.
Хотя в разности пятой подходящей дроби и стоят нули, но все-таки перед ними мы поставили знак «+», так как шестой десятичный знак представлял бы собой цифру, отличную от нуля, и вся дробь имела бы знак «+».
Мы нашли пять приближенных значений тропического года в средних солнечных сутках:
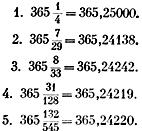
Их анализ показывает следующее:
1. Если вместо принятого нами значения тропического года в 365,24220 средних солнечных суток принять первое полученное нами грубое приближение в 365,25суток, то нужно в течение трех лет считать в году по 365 суток, а па четвертый год 366. Такая система високоса существовала в юлианском календаре.
2. Второе, более точное значение тропического года в З65 и 7/29 суток показывает, что в течение 29 лет придется 7 раз считать годы високосными. Эта система ни разу не находила применения.
3. Еще более точное значение дает величина З65 и 8/33 суток. Эта система была положена в основу персидского календаря, разработанного в XI в. Омаром Хайямом. В ней на каждые 33 года приходится 8 високосных лет.
4. Если за среднюю продолжительность тропического года принять величину З65 и 31/128 суток, то в каждые 128 лет придется 31 год считать високосными. Эта система была применена в календарном проекте И. Г. Медлера.
5. Наконец, следует отметить, что пятая и возможные последующие подходящие дроби никогда в истории всерьез не рассматривались. Они лежат далеко за пределами точности, требующейся для практических надобностей. Однако необходимо помнить, что величина 365,24220 также является приближенной, так как продолжительность тропического года мы в самом начале условились округлить до пятого десятичного знака.
Точность солнечных календарей. Для определения точности любого солнечного календаря можно пользоваться следующей формулой:
![]()
где А — абсолютная величина годичной ошибки в средних сутках, Т — продолжительность тропического года в тех же сутках, m — число простых лет в календарном цикле, n — число високосных лет в том же цикле. Здесь за календарный цикл принимается знаменатель дроби m + n в приведенной формуле. Подставляя в нее соответствующие значения m, n и T, можно составить таблицу, показывающую точность ряда известных нам солнечных календарей:
| Название календаря | m | n | А | Период, в течение которого ошибка достигает целых суток |
| Древнеегипетский | 4 | 0 | —0,24220 | 4 года |
| Юлианский | 3 | 1 | +0,00780 | 128 лет |
| Григорианский | 303 | 97 | +0,00030 | 3280 » |
| Омара Хайяма | 25 | 8 | +0,00022 | 4500 » |
| И. Г. Медлера | 97 | 31 | —0,00001 | 100000 » |