1. Математическая теория лунных и лунно-солнечных календарей. Основные календарные циклы.

Луна и календарь. На самых ранних стадиях развития человеческого общества потребовалось создать единицу измерения времени более крупную, чем сутки. Такая единица была найдена в смене лунных фаз. Поэтому не удивительно, что у большинства древних народов первоначально календарь создавался на основе обнаруженной периодичности в движении Луны. В этом не последнюю роль сыграло и то, что в странах Востока культ Луны имел большое значение в первобытной религии.

Астрономы Востока, особенно вавилонские, достигли больших успехов в изучении Луны и, в частности, в определении времени между двумя новолуниями. Этот период впоследствии получил название синодического месяца, что происходит от греческого слова, означающего «схождение», так как во время новолуний Луна как бы сходится с Солнцем.

Неомения. Точно фиксировать момент новолуния можно только во время солнечных затмений, а они наблюдаются редко. Поэтому пришлось выбрать фазу, близкую к новолунию, а именно наблюдать первое появление лунного серпа после новолуния. Такой момент греки назвали неоменией. Молодая Луна может наблюдаться в сумерках за несколько минут до своего захода. Тот день, в который наблюдался первый заход молодой Луны, и принимался за начало календарного месяца у всех народов, которые вели счет времени по лунному календарю. Промежуток времени от новолуния до неомении зависит как от астрономических, так и от метеорологических обстоятельств. В хронологии он принимается в среднем равным 36 часам. Неомении тщательно наблюдали многие народы древнего мира: вавилоняне, евреи, греки, римляне, индийцы и некоторые другие.

Синодический месяц. Тысячелетия назад было установлено, что в промежутке между двумя последовательными неомениями всегда либо 29, либо 30 дней. Поэтому продолжительность синодического месяца первоначально была определена в 29 ¹/₂ дней, а месяцы календарного года попеременно чередовались по 29 и 30 дней. Первые из них назывались пустыми, а вторые — полными.

Для создания лунного календаря необходимо было установить такую последовательность чередования полных и пустых месяцев, при которой начала этих месяцев всегда приходились на новолуние. Но астрономические новолуния для этой цели не годятся, так как промежуток между двумя последовательными новолуниями колеблется в широком интервале — от 29,25 до 29,83 дня. Причиной этого являются эллиптичность лунной орбиты и смещение лунных узлов. Значит, надо установить среднюю продолжительность синодического месяца, взятую за возможно больший отрезок времени. Для этого можно воспользоваться двумя полными солнечными затмениями, отделенными друг от друга большим интервалом времени. За первое примем одно из древнейших солнечных затмений, о наблюдении которого до нас дошли сведения. Такое затмение произошло 28 мая 585 г. до н. э. в 14 час. 30 мин. по гринвичскому времени. За второе — затмение, которое произошло 22 сентября 1968 г. Нетрудно установить, что между этими двумя солнечными затмениями прошло 932 221,9 дня и за это же время миновало 31 568 лунных месяцев. Тогда для средней продолжительности синодического месяца получаем: 
                                    932 221,9/31 568 = 29,53059

или 29 дней 12 часов 44 минуты 3,0 секунды.

Это значение синодического месяца отличается от величины 29,53058818, принятой в современной астрономии, всего на 0,2 секунды. Для построения лунного календаря такой точности не требуется и достаточно ограничиться пятью десятичными знаками: 29,53059 средних солнечных суток.

Теория лунных календарей. Необходимость в единице времени более крупной, чем месяц, привела к лунному году, состоящему из 12 лунных месяцев. Точная продолжительность астрономического лунного года 354,36706 суток. Приблизительная длина лунного года

29,5 × 12 = 354 дня.

Все нечетные месяцы (1, 3, 5, 7, 9 и 11) содержат по 30 дней, а четные (2, 4, 6, 8, 10 и 12) — по 29 дней. Тогда в календарном году будет тоже 354 дня, так как

6 × 30 + 6 × 29 = 354.

Ошибка, которую мы вводим, принимая месяцы равными 29 и 30 дням, будет постепенно накапливаться и отодвигать первое число месяца, а также первое число лунного года от новолуния.

Основатель ислама Мухаммед (Магомет), узаконивший лунный календарь для правоверных мусульман, предписал каждый новый месяц, как и каждый новый год, обязательно начинать в новолуние, вернее, в неомению. Но как выполнить это требование? Ведь ежегодно фазы Луны смещаются на 0,36706 суток. За 10 лет ошибка составит более чем 3,67 дня, и новолуние уйдет вперед. Чтобы избежать этой неприятности, было решено периодически исправлять лунный календарь, добавляя к некоторым лунным годам лишние сутки, т. е. увеличивать год до 355 дней. Такие годы, аналогично удлиненным годам солнечного календаря, будем называть високосными лунными годами.

Для решения задачи о выборе системы високоса важно было подобрать такое целое число лунных лет, которое наилучшим образом приближалось бы к целому числу дней. Такая задача проще всего может быть решена следующим образом. Продолжительность лунного астрономического года 354,36706 будем последовательно умножать на числа 2, 3, 4 и т. д. до тех нор, пока полученное произведение не подойдет возможно ближе к целому числу.

Наиболее удачными соотношениями являются такие:

354,36706 × 8 = 2834,936, 

354,36706 × 30 = 10631,012.

Только эти два равенства и получили практическое применение во всех действующих лунных календарях. Первое равенство, т. е. 8-летняя продолжительность, получило название «турецкого цикла», а второе, 30-летняя периодичность, — «арабского цикла».

«Турецкий цикл» лунного календаря. В этом цикле 8 лунных лет по 354,36706 дня содержат приблизительно 2835 дней. Но 8 простых лунных лет по 354 дня содержат всего 2832 дня. Поэтому для того, чтобы по прошествии 8 лет новолуния вновь совпали с началом лунного календарного года, необходимо добавить трое суток, т. е. три года цикла сделать високосными, состоящими из 355 дней. Тогда получим новое соотношение:

354 × 5 + 355 × 3 = 2835 дней.

В таком цикле високосные годы надо распределить так, чтобы к концу каждого года ошибка не превышала половины дня. Это достигается только в том случае, если високосные годы придутся на 2-й, 5-й и 7-й годы каждого восьмилетия.

Интересно отметить, что период в 2835 дней состоит из целого числа недель, вследствие чего к концу периода новолуния падают снова на те же дни недели. Это даст возможность составить «вечный» лунный календарь, т. е. такие таблицы, которые в каждом 8-летнем периоде показывают соответствие чисел месяца и дней недели. Такие таблицы по-турецки называются «рузнамэ», что значит «книга дней».

«Арабский цикл» лунного календаря. В этом цикле 30 лунных лет по 354,36706 дня содержат приблизительно 10 631 день. Но 30 простых лет по 354 дня содержат только 10 620 дней. Поэтому за каждые 30 лет новолуние будет запаздывать почти точно на 11 дней. Очевидно, придется к 11 годам каждого 30-летнего цикла прибавлять по одному дню. Тогда 19 простых лет будут содержать до 354 дня и 11 високосных лет по 355 дней.

При определении того, какие годы считать високосными в этом календаре, было принято то же правило, что и при распределении високосных лет в «турецком цикле», а именно: ошибка календаря к концу каждого календарного года не должна превышать 0,5 дня, если предполагать, что в начале цикла она была равна нулю. Учитывая это, наиболее целесообразно считать високосными годами следующие годы 30-летнего цикла: 2-й, 5-й, 7-й, 10-й, 13-й, 16-й, 18-й, 21-й, 24-й, 26-й и 29-й.

Следует еще иметь в виду, что при таком чередовании високосных годов соблюдается обязательное требование, чтобы первое число каждого месяца и начало нового года хорошо совпадало с неоменией, т. е. днем первого появления на небе новой Луны.

Математическая теория лунных календарей. Рассмотренные нами два вида лунных календарей являются только частными случаями. В общем виде задача могла быть решена так же, как она решалась в теории солнечных календарей. В этом случае, исходя из равенства 29,530588 × 12 = 354,36706, нам следует десятичную часть продолжительности лунного года, т. е. величину 0,36706, разложить в непрерывную дробь. Тогда будем иметь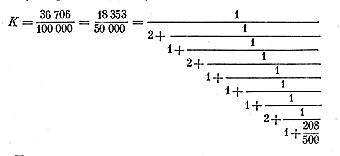

Последовательное решение этого равенства приведет к следующим подходящим дробям:

К = 1/2; 1/3; 3/8; 4/11; 7/19; 11/30; 29/79; 40/109; ...

Здесь значения К = 3/8 и К = 11/30 являются теми подходящими дробями, которые были найдены иным методом для «турецкого» и «арабского» циклов лунных календарей.

Лунно-солнечные календари и их математическая теория. Лунно-солнечные календарные системы намного сложнее как лунных, так и солнечных календарей. Здесь необходимо, чтобы начала календарных месяцев возможно ближе располагались к новолунию, а сумма некоторого числа целых лунных месяцев возможно точнее соответствовала истинной продолжительности тропического года. Таким образом, в лунно-солнечном календаре необходимо согласовать смену лунных фаз с годичным движением Солнца. В основу теории лунно-солнечного календаря положены следующие постоянные величины:

1 тропический год = 365,24220 суток, 
            1 синодический месяц = 29,53059 суток.

Разделив первую величину на вторую, получим

A = 365,24220/29,53059 = 12^{1 087 512}/_{2 953 059}.

Значит, в солнечном году 12 полных лунных месяцев и некоторая дробь.

Аналогично тому, как мы поступали при рассмотрении математической теории как солнечного, так и лунного календаря, полученную простую дробь развернем в непрерывную и получим ряд подходящих дробей. В общем виде эта дробь может быть представлена так:

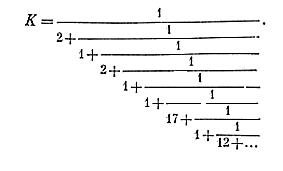
Последовательно решая ее, получим подходящие дроби:

1/2; 1/3; 3/8; 4/11; 7/19; 123/334; 376/1024 и т.д.

Эти дроби дают нам следующие приближенные равенства:

1) 1 солнечный год = 12 ¹/₂ лунного месяца, или 2 солнечных года = 25 лунным месяцам;
2) 1 солнечный год = 12 ¹/₂ лунного месяца, или 3 солнечных года = 37 лунным месяцам;
3) 1 солнечный год = 12 ³/₈ лунного месяца, или 8 солнечных лет = 99 лунным, месяцам;
4) 1 солнечный год = 12 ⁴/₁₁ лунного месяца, или 11 солнечных лет = 136 лунным месяцам;
5) 1 солнечный год = 12 ⁷/₁₉ лунного месяца, или 19 солнечных лет = 235 лунным месяцам;
6) 1 солнечный год = 12 ¹²³/₃₃₄ лунного месяца, или 334 солнечных года = 4131 лунному месяцу.

Можно, конечно, составить еще ряд равенств, но они явно не смогут быть использованы, так как для выравнивания солнечных годов с лунными месяцами потребуются слишком большие промежутки времени. По этой же причине придется отбросить и равенство шестое.

Что касается всех остальных равенств, то каждое из них не только может быть положено в основу лунно-солнечного календаря, но и действительно применялось в истории человечества в ряде календарных систем.

Октаэтерида. Древнегреческий астроном Клеостат в VI в. до н. э. впервые предложил применять 8-летний цикл — октаэтериду. Он основан на следующем равенстве:

8 солнечных лет = 2922 дням.

Но такое же количество дней содержалось в 99 лунных месяцах, в которых 48 было «пустых», т. е. по 29 дней, и 51 «полный», т. е. по 30 дней. Это привело к определению года в 365,25 дня, а синодического месяца — в 29,515 дня.

Так как действительная продолжительность 99 синодических месяцев составляет 2923,53 дня, то ошибка составляла 1,53 дня в 8 лет, или приблизительно 3 дня в 16 лет.

Цикл Метона. Однако наибольшее распространение получило равенство, где подходящей дробью является 7/19. На ней базируется один из основных календарных циклов, получивший название цикла Метона.

Считая, как в юлианском календаре, год равным 365 1/4 суток, имеем такие равенства:

19 солнечных лет = 6939,750 дня, 235 лунных месяцев = 6939,689 дня.

Округляя до целого числа дней, получаем важное равенство:

19 солнечных лет = 235 лунным месяцам = 6940 суткам.

Так как календарные месяцы могут иметь либо 29, либо 30 дней, то можно установить такую интересную зависимость: если взять 110 пустых месяцев (по 29 дней) и 125 полных месяцев (по 30 дней), то в сумме они будут содержать 6940 дней. Но, как мы только что видели, такое же количество дней содержится в 19 солнечных годах.

Впервые это важное положение было установлено еще в 432 г. до н. э. древнегреческим астрономом и математиком Метоном. Оно служит основой почти всех действовавших лунно-солнечных календарей и носит название цикла Метона, а само порядковое число года в 19-летнем цикле получило название золотого числа. Первый день первого метонова цикла относится к 16 июля 432 г. до н. э.

Как лучше всего распределить все 235 месяцев в 19-летнем солнечном цикле? Издавна принято считать 12 лет по 12 лунных месяцев и 7 лет — по 13 месяцев. Эти вставные, т. е. тринадцатые, месяцы получили название «эмболисмических» — от греческого слова, означающего «вставка».

Теперь остается правильно распределить 7 високосных лет в нашем 19-летнем цикле. Чтобы лучше всего согласовать изменение лунных фаз с движением Солнца, древние хронологи прежде всего обратили внимание на подходящие дроби 1/3; 3/8; 4/11; и 7/19. Знаменатели этих дробей подсказали, что високосными годами должны быть 3-й, 8-й, 11-й и 19-й годы цикла. Остальные високосные годы заняли места 6, 14 и 17.

Цикл Калиппа. Древнегреческий астроном Калипп в 330 г. до н. э. усовершенствовал лунно-солнечный календарь, предложив новый календарный цикл. Он знал, что в 19-летнем солнечном цикле не 6940 дней, а только 6939, 75. Поэтому, чтобы учесть оставшуюся ошибку, Калипп решил учетверить цикл:

19 × 4 = 6939,75 × 4 = 27 759 дней.

Значит, в 76 солнечных годах 27 759 дней. Но в таком цикле должно быть уже не 235 лунных месяцев, а 940. Это число месяцев Калипп предложил распределить так: 499 полных (по 30 дней) и 441 пустой (по 29 дней).

Эта весьма удачная поправка привела к уточнению продолжительности лунного месяца, среднее значение которого оказалось равным 27 759/940 = 29,53058 суток, т. е. всего на 0,00026 суток, или на 22 секунды больше принятого в настоящее время.

Поправка Калиппа применялась в древней хронологии, в частности в «Альмагесте» Птолемея. Начальные эпохи 76-летних периодов Калиппа: 28 июня 330 г., 28 июня 254 г., 28 июня 178 г. до п. э. и т. д.

Цикл Гиппарха. Дальнейшее уточнение лунно-солнечных календарных циклов связано с именем Гиппарха. Примерно за 125 лет до н. э. он открыл явление прецессии — перемещения точки весеннего равноденствия навстречу годичному движению Солнца, отчего происходит «предварение равноденствий». Гиппарх установил, что за 150 лет равноденствие сместилось примерно на полсуток. Поэтому он сделал правильное заключение, что длина солнечного года равна не 365,25суток, а на несколько минут короче. Гиппарх считал, что длину четырех калипповых периодов надо укоротить на один день. Тогда получалось равенство: 304 (76 × 4) солнечных года = 3760 (940 × 4) лунным месяцам — 27 759 × 4 - 1 = 111 035 дням.

Это важное равенство позволило Гиппарху получить более точные значения не только синодического месяца, но и тропического года. Предложенная им поправка приводила к такому выводу:

1 солнечный год = 365,24671 дня,

1 лунный месяц =29,53059 дня.

Из этих двух равенств можно заключить, что величина тропического года уже во времена Гиппарха была определена с точностью до 6,5 мин., а средняя продолжительность синодического месяца — с точностью, с какой она используется в современной астрономии.

Следует отметить, что поправка Гиппарха никогда не применялась в календарных системах, а поправка Калиппа применялась только древнегреческими астрономами. Наибольшее распространение в различных календарных системах получили циклы 8-летний и 19-летний. Именно они подробно изложены в знаменитом труде «Памятники минувших поколений», написанном в 1000 г. выдающимся хорезмийским ученым-энциклопедистом ал-Бируни (973—1048).

Лунно-солнечные календарные системы применялись в Вавилоне, Древнем Китае, Иудее, Древней Греции и в Древнем Риме. В наше время лунно-солнечный календарь сохранился в государстве Израиль, а также применяется при вычислении пасхалий.